Avant de commencer à vérifier nos résultats, nous allons addimentionaliser nos équations. Pour cela, nous posons :

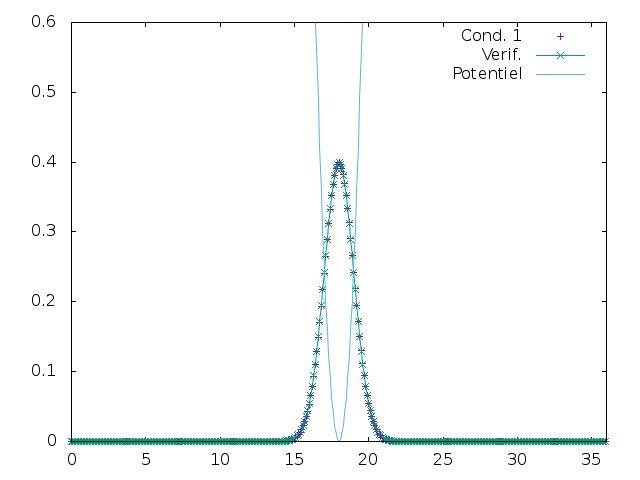
Pour vérifier la validité de notre programme, nous avons utilisé un livre de référence en Mecanique Quantique:

Mecanique Quantique de Cohen - Tannoudji

D'après la théorie quantique, lorsqu'un condensat, ou une particule à l'état fondamental, est piégée dans un piège harmonique, sa fonction d'onde est une fonction Gaussienne.
L'équation du piège harmonique est la suivante:

Après addimentionalisation, nous obtenons: :

Nous cherchons les états propres liés à cet oscillateur harmonique.

Nous addimentionalisons:

Ainsi, si nous mettons une fonction quelconque en entrée de notre programme, nous somme censés rentomber sur la fonction théorique à l'êtat stationnaire. Voici le résultat de notre simulation. Nous avons affichés la fonction de théorique et la fonction stationnaire:

Nous voyons bien que nos deux gausiennes sont confondues. La condition de stabilité est vérifiée

Lorsque g devient grand, nous negligeons les facteurs cinétiques. Notre équation devient donc:

Il faut vérifier la normalisation de la fonction d'onde

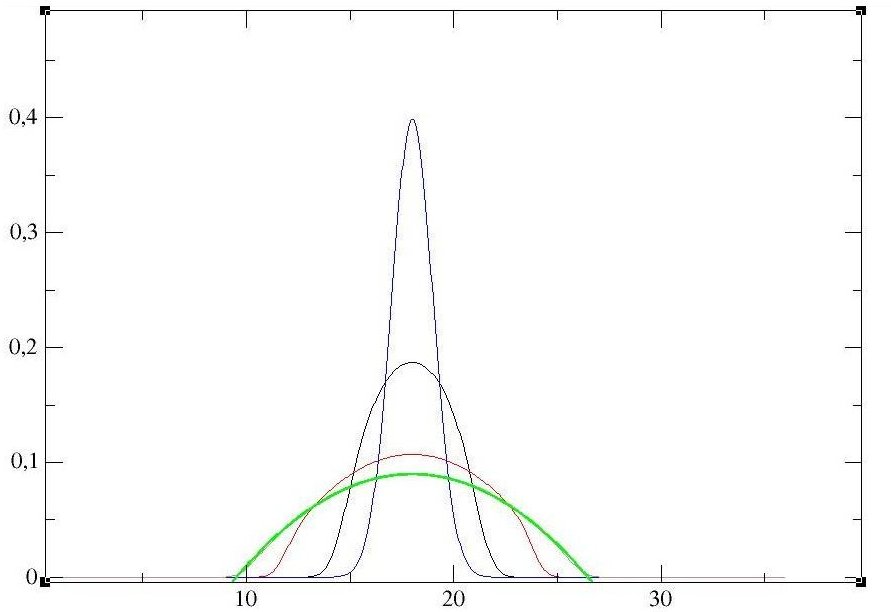
Si nous choisissons g assez grand, nous pouvons trouver une valeur de E en integrant notre fonction sur la taille de notre système. Par exemple, pour g=200, nous trouvons: E~18

Ainsi, si nous traçons notre fonction, en remplacant E, nous devons trouver d'après la théorie de Cohen une parabole inversée (courbe verte)
Nous avons aussi tracés nos fonctions d'ondes avec des g plus petits, pour visualiser l'étalement de la courbe quand g augmente.

Notre courbe stationnaire et la parabole théorique (verte) sont superposées. Nous vérifions bien la théorie trouvée dans le Cohen.

Nous reprenons notre même fonction, (avec un g raisonable). D'après la théorie de Cohen, si nous retirons instantanément le puit, la Gausienne va s'étaler avec une vitesse :

Nous allons, grâce a notre programme dynamique, vérifier cette vitesse d'étalement

Nous affichons donc notre fonction théorique au cours du temps, en même temps que notre fonction d'onde.

Fonction d'onde théorique:

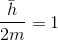
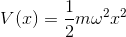
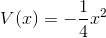
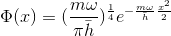
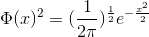
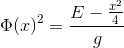
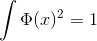
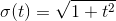
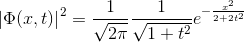
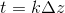avec : ; k étant le pas du programme

Au cours du temps, ces 2 fonctions doivent être confondus