|
Sommaire Haut de page Page précédente Page suivante |
Simulation Stationnaire
Où H est le hamiltonien du système. Ces equations s'obtiennent d'après la rotation de wick. La partie réelle étant indépendante de la partie imaginaire, on fait le choix de n'étudier que la partie réelle de la fonction d'onde. Ce qui nous amène à la relation suivante : Où l'opérateur d'énergie cinétique .gif) et et .gif)
On compare un taux de précision choisi à Ψ(k+1) - Ψ(k). Une fois cette valeur inférieure au taux de précision on considère que le condensat est dans un état stationnaire, on pourra donc récupérer directement la valeur de plus basse énergie.Notons que nous renormalisons la fonction d'onde à chaque pas de temps pour assurer le bon fonctionnement de l'algorithme. On injecte une fonction (normalisé ou non) dans un puit harmonique : on obtient au bout d'un certain temps, en accord avec la théorie, une fonction d'onde normalisée de type gaussien. On généralise ensuite le programme pour deux condensats. Cette fois, le potentiel d'intéraction
g étant le potentiel d'intéraction entre les deux condensats |
|
Copyright © 2015. All rights reserved. By Grammatico Thomas, Dalidet Romain & Mergnat Loïc |
|


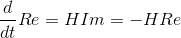
.gif)
.gif)
.gif) dépends à la fois du premier condensat et du deuxième. D'où un système d'équation couplées :
dépends à la fois du premier condensat et du deuxième. D'où un système d'équation couplées :
.gif)
.gif)