Formation des amas de galaxies

Les amas de galaxies furent découverts par les astronomes Hubble et Zwicky, qui en commençant à cataloguer les galaxies, ont déduit qu’elles n’étaient pas réparties aléatoirement dans l’univers mais avaient tendance à s’assembler en différentes structures, c'est à dire les amas. Ces amas de galaxies constituent les pics de surdensité se formant par effondrement gravitationnel à l’intersection des filaments qui jonchent l’univers.

Video montrant l'évolution de la formation de grandes structure en partant de l'Univers très jeune (à très haut redshift)

Dans le modèle hiérarchique de formation des structures ils sont les derniers objets à s’être formés après les galaxies. Les amas de galaxies ont des masses totales qui dépassent souvent quelques 10¹⁴ voir 10¹⁵ fois la masse de notre soleil et ont des tailles typiques de quelques Mpc. Ils sont constitués de matière noire (environ 84% de leur contenu en masse), de gaz composé principalement d’atomes ionisés d’hydrogène et d’hélium (12%) et de galaxies (4%).

Interêt cosmologique

Les amas sont donc les objets gravitationnellement liés les plus grands qui ont atteint un état d’équilibre. Grâce à eux nous pouvons témoigner de la formation des amas même dans l’Univers d’aujourd’hui: ils montrent pour une grande partie, des sous-structures qui peuvent être identifiées comme la fusion avec d’autres groupes de galaxies ou d’amas. Ce sont d’excellents traceurs de la distribution de matière dans l’Univers, ils offrent une sonde pertinente pour tester la formation des structures et permettent en même temps de poser certaines contraintes sur les paramètres cosmologiques. Ils peuvent être observés à différentes longueurs d’onde, du domaine radio au domaine X, chacune d’entre elles étant sensible à différents processus physiques.

Effet Sunyaev Zel'dovich

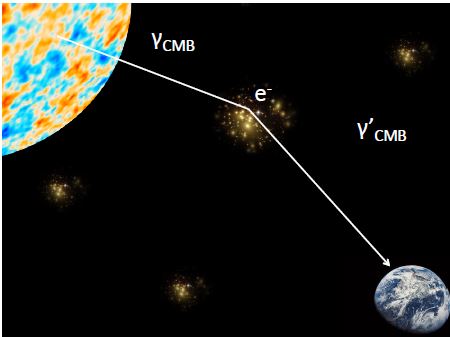
Effet SZ

Figure 1 - Vue schématique de l’interaction Compton inverse d’un photon du CMB sur le gaz chaud d’électrons contenu au sein d’un amas. Il s’agit de l’effet Sunyaev-Zel’dovich

En traversant l'Univers depuis l'instant du découplage jusqu'à maintenant, le rayonnement du fond diffus cosmologique a interagi avec les grandes structures de l'Univers que sont les amas de galaxies. Comme nous l'avons vu dans la partie précédente, les amas de galaxies sont des structures très massives. Environ 12% de la masse de l'amas se trouvent sous forme de gaz distribué dans toute la structure. Ce gaz, dit intra-amas, peut atteindre des températures de plusieurs keV (soit quelques 10⁷ K). A ces températures, le gaz émet dans le domaine des rayons X par Bremsstrahlung. Mais nous n’avons pas seulement un rayonnement dû au freinage des électrons dans le voisinage des ions. Les électrons peuvent eux-mêmes diffuser les photons du CMB par diffusion Compton inverse. C'est ce processus de diffusion Compton inverse qui est appelé effet Sunyaev-Zel'dovich (noté effet SZ).
En réalité, il n'existe pas qu'un seul effet SZ mais plusieurs effets SZ résultants tous du même processus de diffusion Compton inverse. Cependant, ces effets n'ont pas la même origine physique et possèdent des signatures spectrales différentes. Dans le cade de notre projet nous nous intéresserons uniquement à l’effet thermique (tSZ).
L’effet thermique est le plus intense des effets SZ, il consiste en un transfert d’énergie entre les électrons du gaz chaud et les photons du CMB. Il en résulte une modification du spectre électromagnétique du CMB à la position des amas de galaxies.

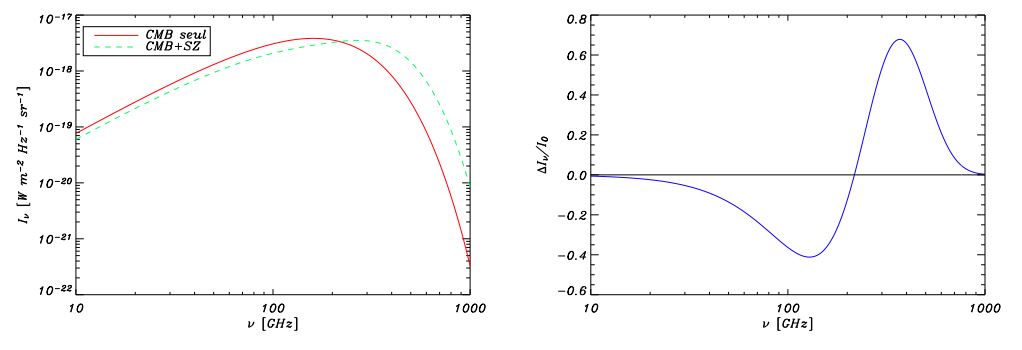
Figure 2 - A gauche : la représentation du spectre CMB (type corps noir) (trait plein rouge) ainsi que le spectre distordu par effet SZ en fonction de la fréquence. A droite : il s’agit de la différence des deux spectres de la figure de gauche : c’est donc le spectre de la distorsion caractéristique de l’effet SZ.

On observe que les principales caractéristiques de cette distorsion sont d’être nulle à ∼217 GHz, négative pour des fréquences d’observations inférieures et positive pour des fréquences supérieures.

La dépendance spectrale de l’effet tSZ relativement au CMB peut se calculer à partir de l’équation de Kompaneets qui décrit la variation de la densité de photons en fonction de leur énergie lors de leur diffusion. La dépendance spectrale est donnée par :

$$f(x,T_e)=\frac{x^{4}e^{x}}{(e^{x}-1)^{2}}(x\times coth \left(\frac{x}{2}\right)-4)(1+\delta_{tSZ} (x,T_e))$$

Et avec x la fréquence adimensionnelle : $$x=\frac{h\nu}{k_{B}\times T_{CMB}}$$

et avec h la constante de Planck, k_b la constante de Boltzmann, ν la fréquence d’observation et T_CMB la température du CMB. Le terme de droite représente des corrections relativistes que l’on négligera car très petites devant notre échelle (de l'ordre de 10% pour les amas les plus chauds).

L’expression de la variation de brillance en direction d’un amas de galaxies est donnée par : $$\frac{\Delta I_{tSZ}}{I_0}=yf(x,T_e)$$ avec I₀ l'intensité du CMB. On voit alors que l’amplitude de l’effet est caractérisée par le seul paramètre y appelé paramètre de Compton. Ce paramètre donne une mesure de la pression électronique intégrée sur la ligne de visée (sans unité) telle que : $$y=\frac{\sigma_T}{m_{e}c^2} \int{P_{e}dl}$$ avec:

σ_T

m_ec²

P_e

L’autre grande caractéristique de l’effet SZ est son indépendance au redshift. En effet, les seules grandeurs qui interviennent sont des caractéristiques propres à l’amas lui-même. En d’autres termes, un même amas produit exactement le même effet qu’il se trouve à z = 0.05, z = 0.5 ou z = 1.5, en dehors du fait que la taille de l’amas sur le ciel est nécessairement plus faible quand son redshift augmente. Ceci fait de l’effet SZ l’outil idéal pour permettre la découverte d’amas distants.

Figure 3 – Cette frise résulte de l’assemblage des cartes de l’amas connu et proche Abell 2319, observé dans 3 bandes de fréquence de Planck. Le signal SZ (tâche centrale) est indiqué en bleu lorsque l’observation du CMB indique un manque de photons, en rouge lorsqu’on observe un excès et le signal est nul pour 217 GHz.

Observations

Dans notre cas, pour détecter l’effet SZ, deux bandes d’observations nous sont accessibles :

- 150 GHz (2mm): ce qui correspond presque à un minimum sur la figure 2, très caractéristique et parfait pour les observations (moins de bruit);

- 260 GHz (1.2mm): où le signal est positif, mais moins favorable que la possibilité précédente à cause du bruit.

Figure 4 – Télescope de l’IRAM de 30 mètres

L'utilisation de télescopes optiques ne permet pas d'étudier tous les éléments constitutifs de l'Univers. C’est pourquoi NIKA2, qui est l’un des instruments du télescope de l’IRAM (figure 4) est utilisé pour la détection du signal SZ.
Basé sur une nouvelle technologie, des détecteurs supraconducteurs maintenus à une température très basse (0.15 Kelvin soit -273 °C), NIKA2 est d'une grande sensibilité.
Grâce à sa haute vitesse de cartographie, ses capacités de polarisation et sa haute résolution angulaire (12 et 18 arcsec) NIKA2 sera capable de révolutionner les observations dans le domaine millimétriques.

Contaminants

Des effets « polluants » peuvent néanmoins venir contaminer les observations.

L’effet de lentille gravitationnelle

Le bruit

Effets instrumentaux