Relation entre la masse et la pression

Au centre des amas de galaxies se trouve un puits de potentiel contenant de la matière noire. Sous l'effet de la gravité, le gaz et les galaxies se trouvant au voisinage proche de l'amas vont être attirés par le centre. Dès lors, la pression de l'amas augmente au centre par équilibre hydrostatique. Il existe donc une relation de proportionnalité entre la pression et la masse : on dit que la pression trace la masse. Dans le cadre de ce projet, nous avons un profil de pression assez simple, notre amas est relaxé.

Profil de pression universel

La première partie de notre programme se caractérise par le calcul de la pression du gaz de notre amas de galaxies, en entrant la masse de l'amas ainsi que son redshift. La formule utilisée a été trouvée suite à des observations.
Dans notre simulation, nous avons décidé de choisir les constantes établies par Planck sur un échantillon de 62 amas proches pour avoir un profil de pression universel, et donc avoir un profil qui est compatible quelle que soit la masse de l’amas choisie. $$P_{e}(r)=\frac{P_0}{\left(\frac{r}{r_p}\right)^{c}\times\left(1+(\frac{r}{r_p})^{a}\right)^{\frac{b-c}{a}}}$$

    - Pe(r) pression de l’amas dépendant de son rayon
    - Po constante de normalisation
    - rp rayon caractéristique (en kpc)
    - r rayon variant de 0.0 à 5*R500 dans notre cas
    - a la pente du profil à des rayons r environ égale à rp
    - b la pente du profil à des rayons r supérieur à rp
    - c pente du profil à des rayons r inférieur à rp
    - R500 rayon pour lequel la densité de l'amas est 500 fois la densité critique de l'Univers.
$$R_{500}=\left[\frac{M_{500}}{500\times \rho_c\times (\frac{4\pi}{3})}\right]^{\frac{1}{3}}$$

Cette partie de programmation nous a permis d’obtenir la pression normalisée de notre amas suivant le rayon de celui-ci.
On s'attend à ce qu'elle soit maximale au cœur de l’amas et diminue de plus en plus lorsqu’on s’en éloigne.

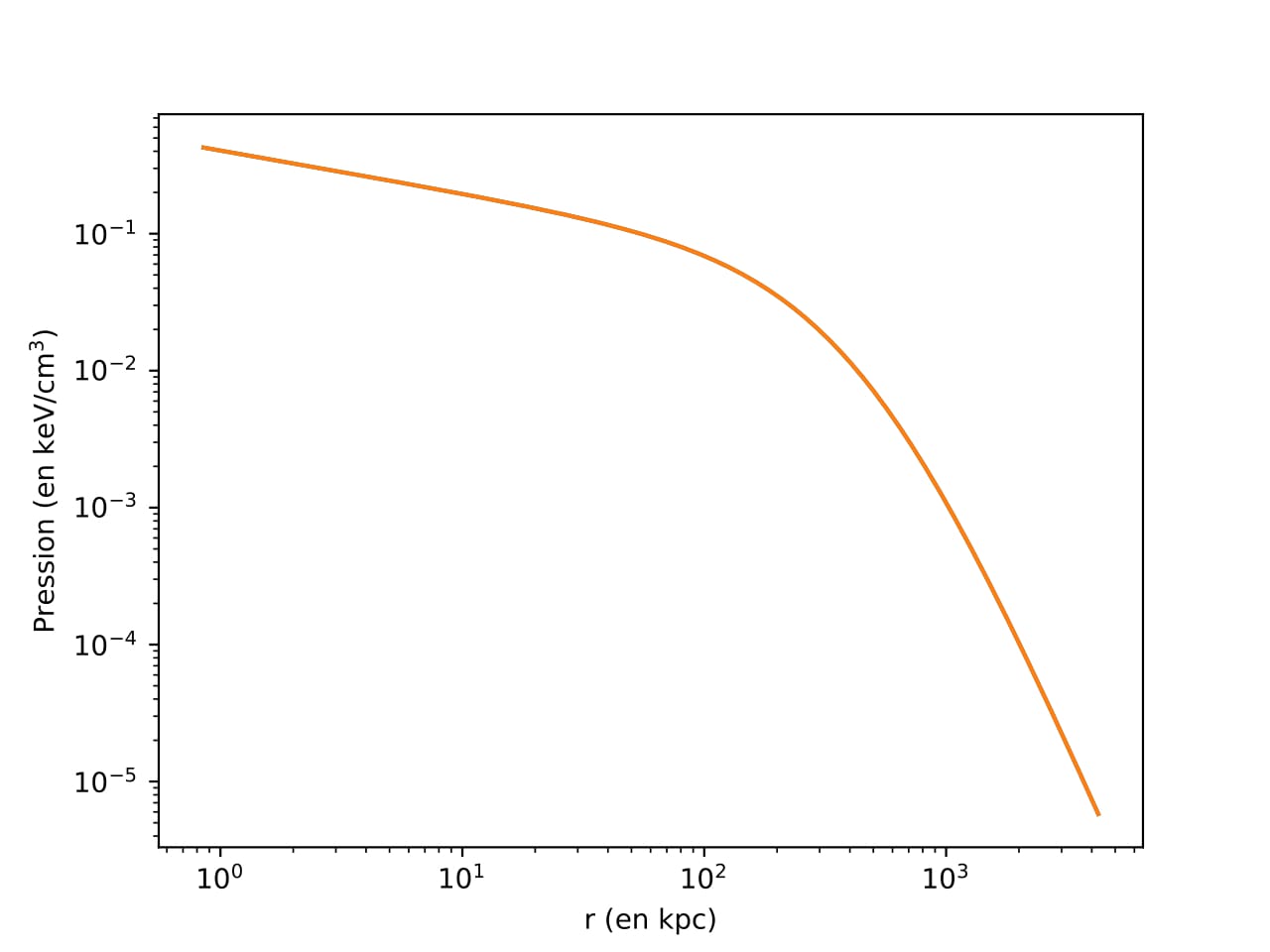
Figure 5 - Evolution de la pression dans un amas en fonction du rayon pour des paramètres de Planck.


Différents types de profils existent, notamment un profil pour les amas relaxés. En fonction du profil choisi, les paramètres qui décrivent la pression changent, l’allure de la courbe évolue :

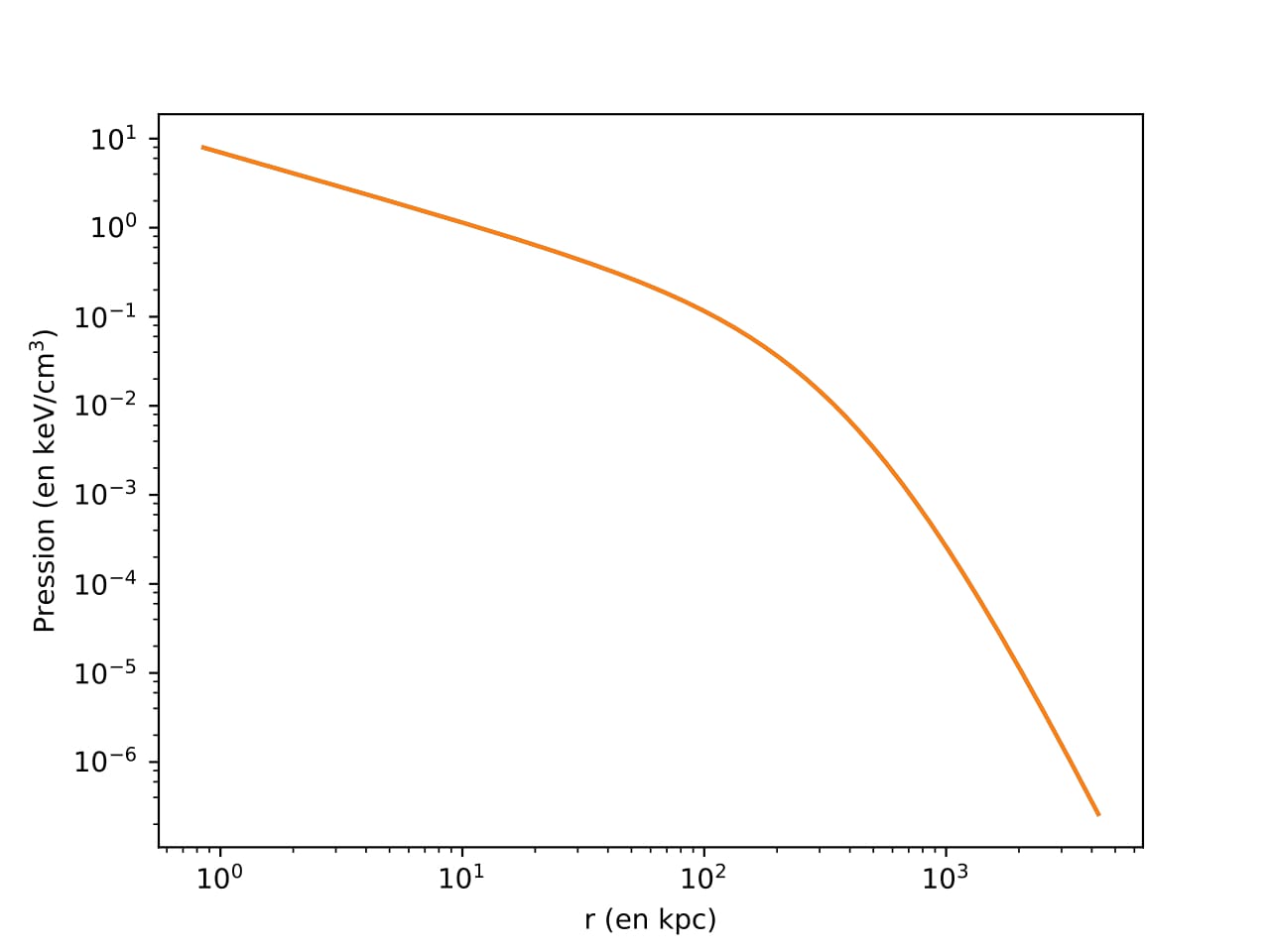
Figure 6 - Evolution de la pression dans un amas en fonction du rayon pour des paramètres cool core


En comparant les deux graphiques, on voit qu’en s’éloignant du centre la pression dans un amas relaxé diminue plus rapidement que dans un amas dont la pression est décrite par les paramètres de Planck, plus adaptés aux amas perturbés.
Suite à cela, nous avons pu calculer le paramètre de Compton et la brillance associés à l’amas observé.

Intégration

Paramètre de Compton
Comme notre modelisation est une modélisation parfaite (aucun bruit ou contaminant) à géométrie sphérique, le paramètre de Compton décrit précédemment peut s'écrire:$$y(R)=\frac{2\sigma_{T}}{m_{e}c^2} \int_{R}^{R_{max}} P_{e}(r)\times\frac{r}{\sqrt{r^{2}-R^{2}}}dr$$ Ainsi, la constante 2 apparait car on passe d’une intégrale de -∞ à +∞ à une intégration entre deux nombres finis. On suppose ici que Rmax ne tend pas forcément vers l’infini mais que l’extension de l’amas se limite à une valeur finie égale dans notre cas à 5.0*R500.
Ceci est considéré comme vrai si on suppose que la contribution au signal des régions lointaines est négligeable et que le gaz peut être considéré comme n’appartenant plus à l’amas pour un certain rayon.

Figure 7 - Schéma représentant le rayon projeté R et le rayon physique r.


On fait l'intégration sur la ligne de visée, en regardant l'amas du dessus on va voir un grand rayon R projeté sur le ciel, mais en pratique le rayon physique de l'amas est r qui pour notre calcul doit être supérieur à R comme on peut le voir sur la figure ci-dessus. Pour finir, pour des raisons d'exactitude, nous avons décidé de réaliser l'intégrale avec la méthode des trapèzes, plus simple à réaliser et plus précise que la méthode des rectangles.
L'échantillonage de r se fait alors de façon logarithmique, nous pouvons donc dire que le pas sur l'intégration dr est optimisé.

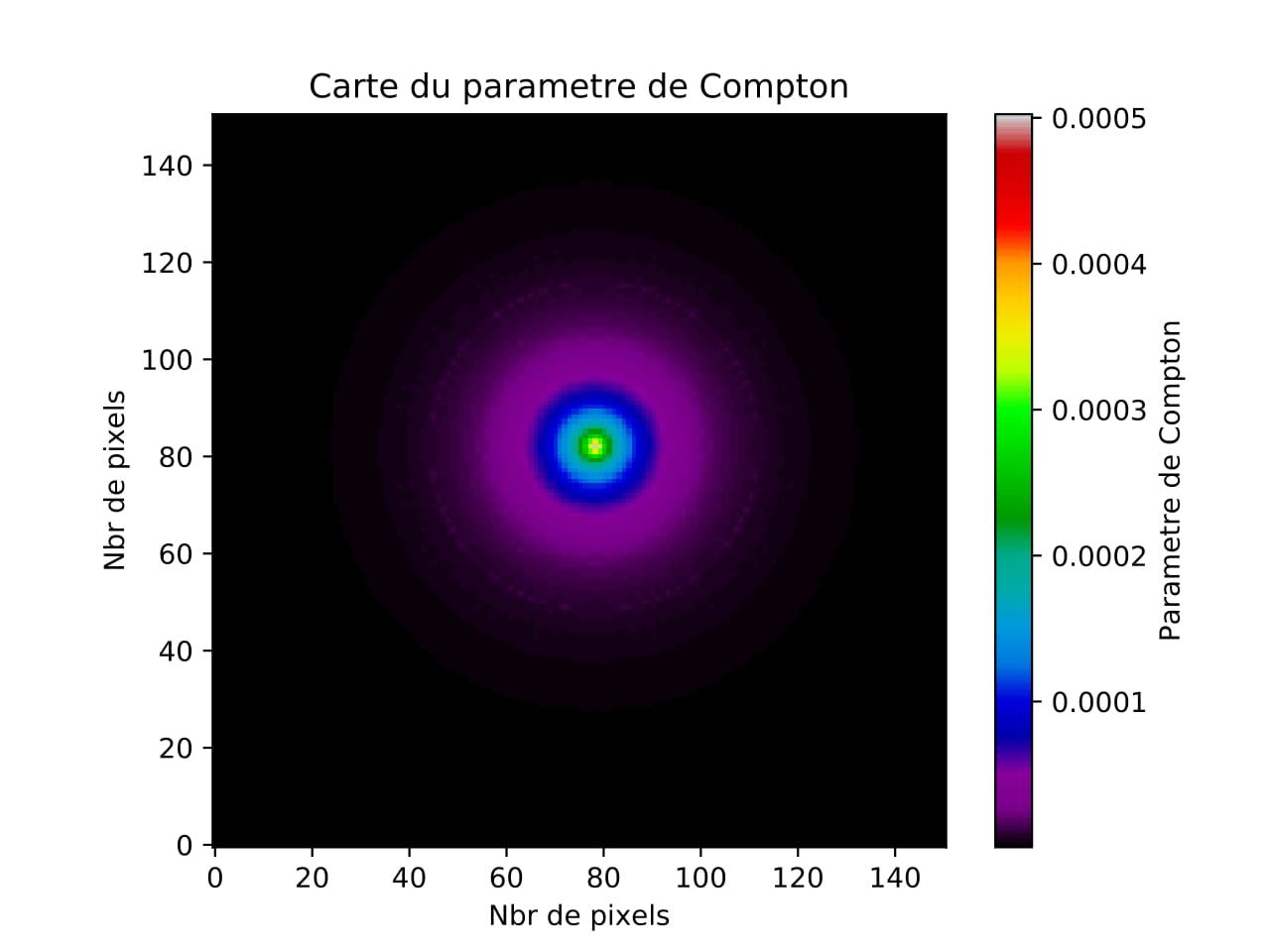
Figure 8 - représentation du paramètre de Compton en fonction du rayon (en pixel).


Par la suite nous avons converti les pixels en seconde d'arc. Cependant notre objectif est de comparer notre carte à celles faites par observations et qui sont des cartes de brillance.


Brillance
Contrairement au paramètre de Compton, le calcul de la brillance est plus simple et rapide à réaliser. La brillance est donnée par : $$\Delta I_{tSZ}=yf(x,T_e)\times I_{0}$$ Dans notre cas, cette formule peut-etre simplifiée assez facilement. En effet, le produit des coefficients muliplicatifs à notre paramètre de Compton y est égale à -10.9 (en Jy/beam) pour NIKA. Cette simple multiplication nous permet de passer du parametre de Compton, à la brillance, quantité réelle et mesurable avec notre telescope pour chaque amas observé.

Validation

Cette partie du programme nous permet simplement de vérifier que notre intégrale numérique fonctionne correctement et d’obtenir la précision sur notre calcul. Nous avons donc introduit une nouvelle fonction analytique appelée « Beta model ». Dans le cas du Beta model, le paramètre de Compton s'écrit : $$y(R)=\sqrt{\pi}r_p\times\frac{\Gamma\left(\frac{3}{2}\beta-\frac{1}{2}\right)}{\Gamma\left(\frac{3}{2}\beta\right)}\left[1+\left(\frac{R}{r_p}\right)^2\right]^{\frac{1}{2}-\frac{3\beta}{2}}$$ et $$P_e(r)=P_0 \left(1+\left(\frac{r}{r_p}\right)^2\right)^{\frac{-3\beta}{2}}$$ β définissant la pente.
Lorsque l’on appelle notre fonction principale, nous avons introduit un paramètre qui nous donne la possibilité de choisir notre modèle : analytique ou numérique. Le modèle analytique est essentiellement fait pour tester notre code, c’est le numérique que nous allons surtout utiliser car il est beaucoup plus évolué et permet de mieux décrire la pression.

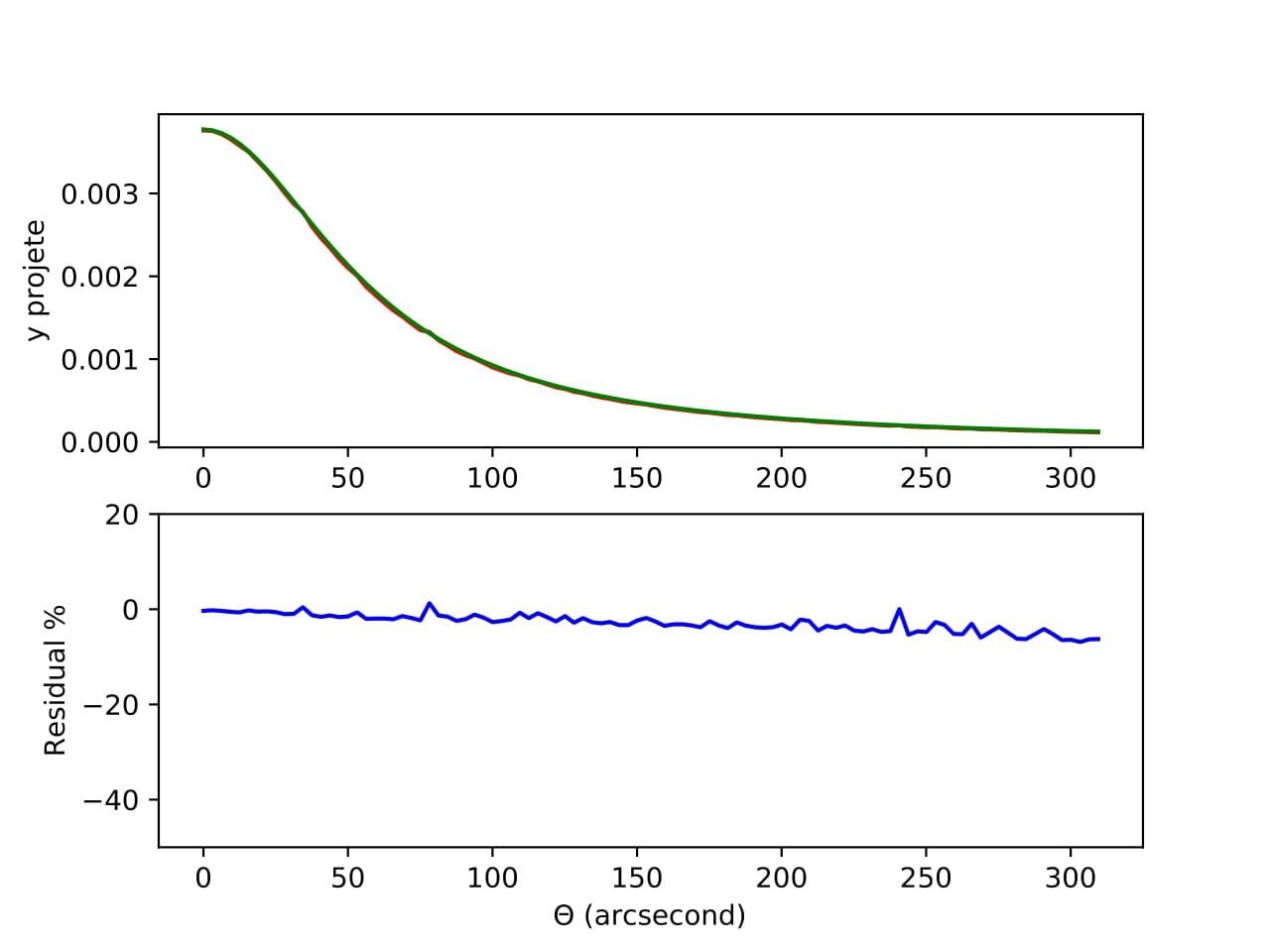
Figure 9 – En vert : la courbe du paramètre de Compton en fonction du rayon en seconde d'arc attendue, en rouge : la courbe de notre fonction analytique, en bleu : le résidu entre les deux.


On constate que le résidu ne dépasse pas 10% pour des grands rayons. Grâce à la fonction analytique on peut donc conclure que notre fonction numérique est valide.

Obtention des Cartes

Dans la dernière partie de notre programme, nous avons tracé les différentes cartes de notre modèle et les cartes issues d'observations de plusieurs amas.
Pour optimiser la comparaison entre les deux modèles :

    - Nous définissons les coordonnées du centre de l'amas sur notre modèle dans le but de pouvoir le déplacer suivant la position du centre de l’amas observé via le télescope.
    - On choisit un nombre de pixel identique entre les deux cartes.
    - Un choix d’unité adéquat pour un représentation dans le domaine abordé.
Dans notre cas, les cartes obtenues représentent la brillance (en mJY/beam) en fonction du rayon de l’amas (en degrés et ses sous unités en seconde d'arc). Notre programme prend en entrée la masse d'un amas et son redshift correspondant. Une fois toutes les étapes effectuées, nous obtenons donc une carte ne dépendant que de la masse et du redshift qui est connu pour chaque amas.