The new chaotic pendulum

A more detailed study of the chaotic pendulum
Poincaré section

To characterise our system's behaviour, we will need to use a Poincaré section ^{[ref1] [ref2]}. The Poincaré sections are subspaces that are reccurently and transversally crossed by the system.
In our case, the chosen Poincaré is a part of the $yOz$ plan which, when passed through by the mass, will read the values of $\theta$ and $\dot{\theta}$.
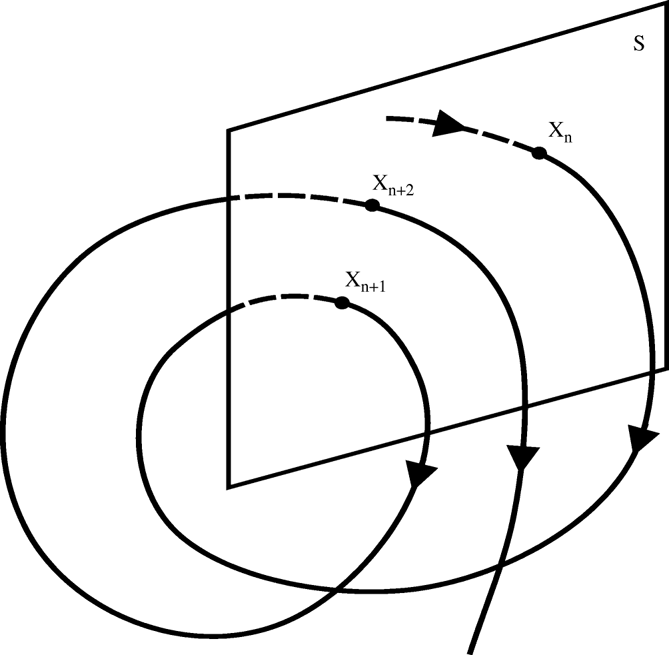After having taken a significant amount of points, we may trace our Poincaré section's graph. This graph may be :

• a unique point: the system is periodic;
• a small amount of points: the system is periodic;
• a closed curve: the system is quasi-periodic;
• a cloud of points: the system is chaotic.

^[ref]

Here are some examples of Poincaré sections :

Quasiperiodic system Image LASIN, uni-lj $[1]$	Chaotic system Image N. De Leon $[2]$

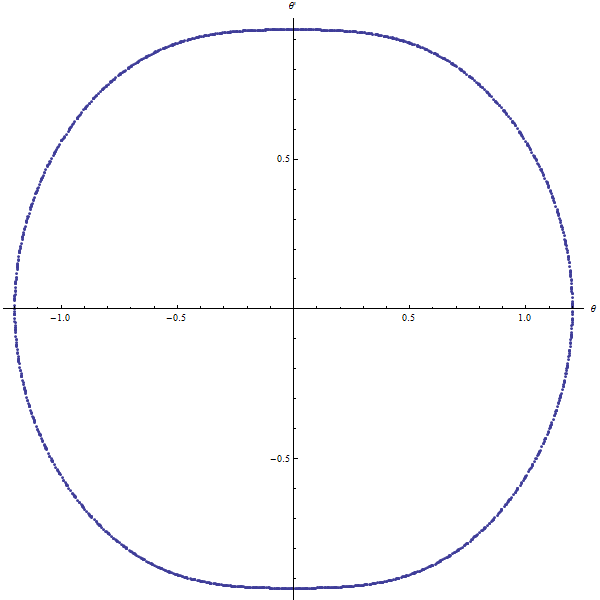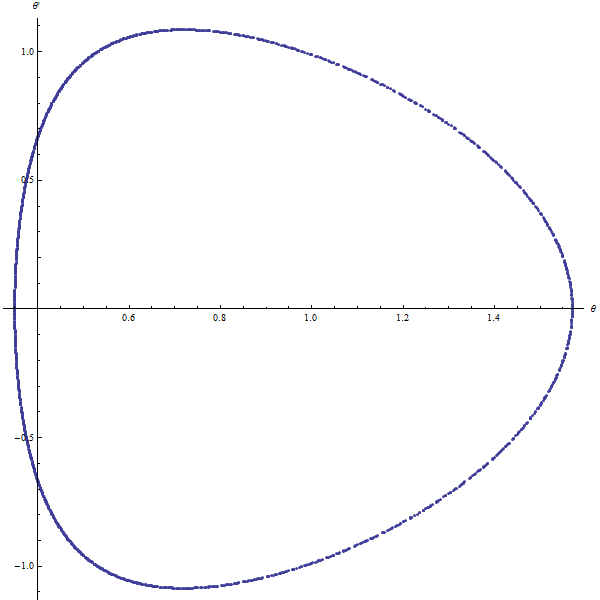spherical pendulum $(\alpha=0)$	spherical pendulum

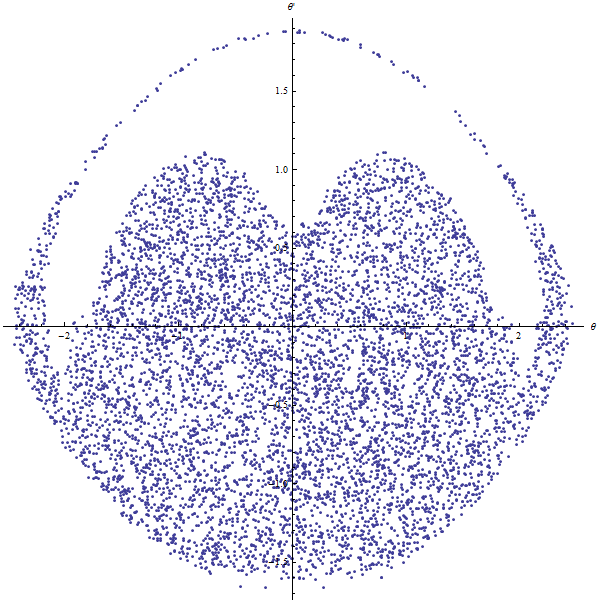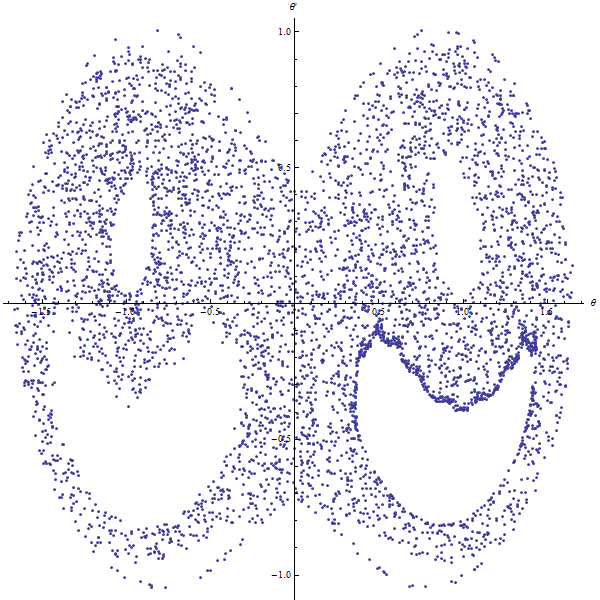chaotic pendulum	chaotic pendulum