The new chaotic pendulum

A more detailed study of the chaotic pendulum
Stability study

To determine whether a fixed point is stable or unstable, we are going to do a linear stability analysis : we place ourselves on the fixpoint, to which we add a small perturbation. The study of the perturbation's evolution will inform us on the fixpoint's stability.
We will study two fixed points.

Study of a first fixpoint

We begin by studying the fixpoint $\theta = \alpha \; , \; \varphi = \frac{\pi}{2}$. We add a perturbation : $\theta = \alpha + \theta _1\; , \; \varphi = \frac{\pi}{2} + \varphi _1 \;$, where $\theta _1 , \varphi _1 \ll 1$. After linearisation and simplification, we get :

$$ \left \{ \begin{eqnarray*} \ddot{\theta _1} &=& -\theta _1 \\ % \ddot{\varphi _1} &=& -\frac{1}{1+\frac{\beta}{\sin ^2 \alpha}}\varphi _1 \end{eqnarray*} \right . $$

We recognise here the equations of an harmonic oscillator for each variable – thus we can deduce that the fixpoint is stable.

Study of a second fixpoint

Let's now study the case of the fixpoint $\theta = \pi , \varphi = 0$. Proceeding as we did for the first fixpoint, we find the following equations :

$$ \left \{ \begin{array}{r c l} \ddot{\theta _1}&=& \theta _1 \cos \alpha -\varphi _1 \sin \alpha \\ % \ddot{\varphi _1}&=& -\frac{\sin \alpha}{\beta}\theta _1 \end{array} \right . $$

We will now integrate numerically those coupled equations and draw the graphs $\theta _1 (t)$ and $\varphi _1 (t)$ to see how the perturbations evolve. We get these two graphs :

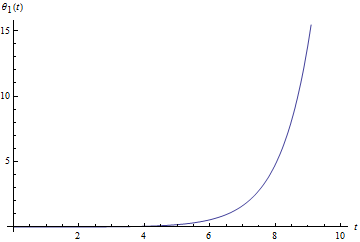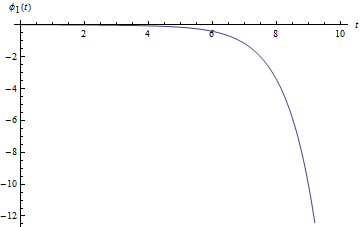Evolution of the perturbation $\theta _1 (t)$	Evolution of the perturbation $\varphi _1 (t)$

We can see that the two perturbation diverge : this fixpoint is unstable.