The new chaotic pendulum

Preliminary study
case of the inclined pendulum

We can now begin to study the bended pendulum. We add another parameter : the pendulum is inclined by an angle $\alpha$ in the $yOz$ plan, with respect to the direction of the gravity $\vec{g}=-g \vec{e_z}$.
Finally, it is the same as considering that $\vec{g}$ has changed its direction. We will thus see this angle in the equations we are going to calculate.

Positions and speeds

Let us begin by seeking the mass' coordinates and corresponding speeds, with respect to the angles $\theta$ and $\varphi$ : $$ \left \{ \begin{array}{r c l} x & = & l \sin \theta \cos \varphi \\ y & = & l \sin \theta \sin \varphi \\ z & = & -l \cos \theta \end{array} \right . \; \Rightarrow \; \left \{ \begin{array}{r c l} \dot{x} & = & l (\dot{\theta} \cos \theta \cos \varphi - \dot{\varphi} \sin \theta \sin \varphi ) \\ \dot{y} & = & l (\dot{\theta} \cos \theta \sin \varphi + \dot{\varphi} \sin \theta \cos \varphi )\\ \dot{z} & = & l \dot{\theta} \sin \theta \end{array} \right . $$ We notice that these are the same equations as the ones we found in the previous case.

energies, Lagrangian, movement equations

We may then find the potential and kinetic energies, and thus the corresponding Lagrangian $\mathcal{L}$. This time, the potential energy's exepression will change : :
$$ \begin{eqnarray*} E_p & = & -\vec{P}\cdot\vec{r}=(mg\cos\alpha\ \vec{e_z}-mg\sin\alpha \ \vec{e_y})\cdot(z\vec{e_z}+y\vec{e_y}) \\ & = & (mg\cos\alpha\ \vec{e_z}-mg\sin\alpha\ \vec{e_y})\cdot(-l\cos\theta\ \vec{e_z}+l\sin\theta\sin\varphi\ \vec{e_y})\\ & = & -mgl(\sin\theta\sin\varphi\sin\alpha+\cos\theta\cos\alpha) \\ E_k & = & \frac{1}{2}m v^2=\frac{m}{2}(\dot{x}^2+\dot{y}^2+\dot{z}^2)=\frac{m l^2}{2}(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta) \\ \\ \\ \mathcal{L} & = & \frac{m l^2}{2}(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta) + mgl(\sin\theta\sin\varphi\sin\alpha+\cos\theta\cos\alpha) \end{eqnarray*}\\ $$

From this we deduce the Euler-Lagrange equations for the inclined pendulum :
$$ \begin{eqnarray} \frac{\partial \mathcal{L}}{\partial \theta} & = & \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\theta}} \; \Rightarrow \; \ddot{\theta}=\dot{\varphi}^2\sin\theta\cos\theta+\frac{g}{l}(\cos\theta\sin\varphi\sin\alpha-\sin\theta\cos\alpha) \\ % \frac{\partial \mathcal{L}}{\partial \varphi} & = & \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\varphi}} \; \Rightarrow \; \ddot{\varphi}=\frac{g}{l\sin\theta}\cos\varphi\sin\alpha-2\dot{\theta}\dot{\varphi}\cot\theta \end{eqnarray} $$

Integrating the equations

We can now integrate numerically the new-found coupled equations : we get the following trajectories, which of course depend of the initial conditions we chose :

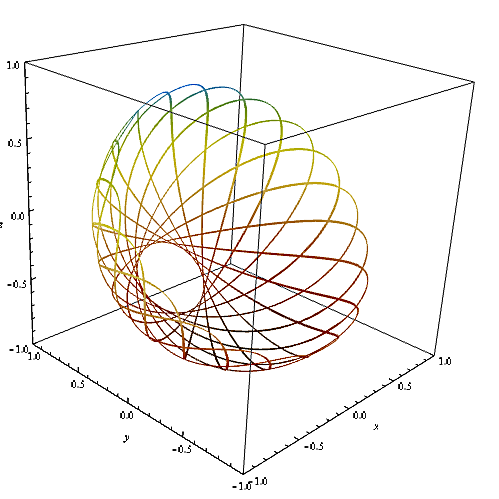
We can see that this case is very close to the spherical pendulum : it is a spherical pendulum, but bended by an angle $\alpha$. We see that it simply comes from the minimal of potential's shifting : the gravity being bended by an angle $\alpha$ with respect to the $z$ axis, the minimal of potential will be shifted by an angle $\alpha$ too.

In the present case, we still don't observe a chaotic behaviour.