Le nouveau pendule chaotique

Etude préliminaire – cas du pendule sphérique incliné

On se penche maintenant sur le cas du pendule sphérique incliné. On ajoute encore un paramètre : on incline le système d'un angle $\alpha$ dans le plan $yOz$ par rapport à la direction prise par l'accélération de la pesanteur $\vec{g}=-g \vec{e_z}$.
Au final, cela revient à considérer que $\vec{g}$ a changé de direction. On verra donc apparaître cet angle dans les calculs des nouvelles équations.

Positions et vitesses

Commençons par chercher les coordonnées de la masse en fonction ds angles $\theta$ et $\varphi$, ainsi que les vitesses correspondantes : $$ \left \{ \begin{array}{r c l} x & = & l \sin \theta \cos \varphi \\ y & = & l \sin \theta \sin \varphi \\ z & = & -l \cos \theta \end{array} \right . \; \Rightarrow \; \left \{ \begin{array}{r c l} \dot{x} & = & l (\dot{\theta} \cos \theta \cos \varphi - \dot{\varphi} \sin \theta \sin \varphi ) \\ \dot{y} & = & l (\dot{\theta} \cos \theta \sin \varphi + \dot{\varphi} \sin \theta \cos \varphi )\\ \dot{z} & = & l \dot{\theta} \sin \theta \end{array} \right . $$ On remarque qu'il s'agit des mêmes équations que dans le cas précédent.

énergies, Lagrangien, équations du mouvement

On peut alors trouver les énergies potentielle et cinétique, et donc le Lagrangien $\mathcal{L}$ correspondant. Cette fois-ci l'expression de l'énergie potentielle sera différente :
$$ \begin{eqnarray*} E_p & = & -\vec{P}\cdot\vec{r}=(mg\cos\alpha\ \vec{e_z}-mg\sin\alpha \ \vec{e_y})\cdot(z\vec{e_z}+y\vec{e_y}) \\ & = & (mg\cos\alpha\ \vec{e_z}-mg\sin\alpha\ \vec{e_y})\cdot(-l\cos\theta\ \vec{e_z}+l\sin\theta\sin\varphi\ \vec{e_y})\\ & = & -mgl(\sin\theta\sin\varphi\sin\alpha+\cos\theta\cos\alpha) \\ E_c & = & \frac{1}{2}m v^2=\frac{m}{2}(\dot{x}^2+\dot{y}^2+\dot{z}^2)=\frac{m l^2}{2}(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta) \\ \\ \\ \mathcal{L} & = & \frac{m l^2}{2}(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta) + mgl(\sin\theta\sin\varphi\sin\alpha+\cos\theta\cos\alpha) \end{eqnarray*}\\ $$

On en déduit les équations d'Euler-Lagrange du pendule incliné :
$$ \begin{eqnarray} \frac{\partial \mathcal{L}}{\partial \theta} & = & \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\theta}} \; \Rightarrow \; \ddot{\theta}=\dot{\varphi}^2\sin\theta\cos\theta+\frac{g}{l}(\cos\theta\sin\varphi\sin\alpha-\sin\theta\cos\alpha) \\ % \frac{\partial \mathcal{L}}{\partial \varphi} & = & \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\varphi}} \; \Rightarrow \; \ddot{\varphi}=\frac{g}{l\sin\theta}\cos\varphi\sin\alpha-2\dot{\theta}\dot{\varphi}\cot\theta \end{eqnarray} $$

Intégration des équations

On intègre numériquement les équations couplées obtenues plus haut : on obtient les trajectoires suivantes, dépendant évidemment des conditions initiales imposées:

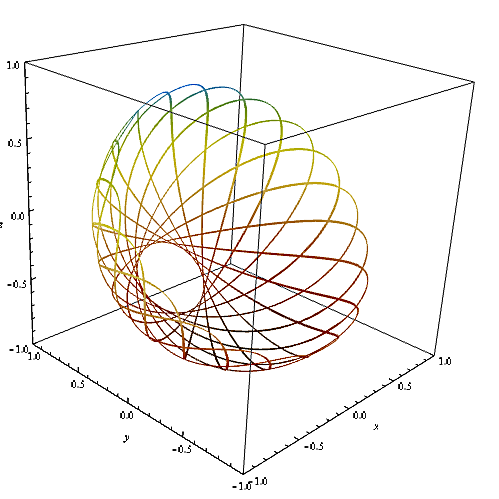
On peut voir que ce cas est très similaire à celui du pendule sphérique : il s'agit d'un pendule sphérique qui est simplement incliné d'un angle $\alpha$. On voit que cela vient simplement d'un déplacement du minimum de potentiel : la gravité étant inclinée d'un angle $\alpha$ par rapport à l'axe $z$, le minimum de potentiel du système sera lui aussi déplacé d'un angle $\alpha$.

Dans le cas présent, on n'observe pas encore de comportement chaotique.