Le nouveau pendule chaotique

étude préliminaire – cas du pendule simple

Positions et vitesses

Nous allons commencer l'étude du pendule par le cas le plus trivial que l'on puisse rencontrer: le pendule simple. Il s'agit en fait d'une simple masse $m$ oscillant sans frottement dans un plan et suspendue au bout d'un fil de longueur $l$ et de masse négligeable. Le tout est soumis à l'accélération de la gravité $\vec{g}$.

Commençons par chercher les coordonnées de la masse en fonction de l'angle $\theta$, ainsi que les vitesses correspondantes: $$ \left \{ \begin{array}{r c l} x & = & l \sin \theta \\ y & = & 0 \\ z & = & -l \cos \theta \\ \end{array} \right . \; \Rightarrow \; \left \{ \begin{array}{r c l} \dot{x} & = & l \dot{\theta} \cos \theta \\ \dot{z} & = & l \dot{\theta}\sin \theta\\ \end{array} \right . $$

énergies, Lagrangien, équation du mouvement

On peut alors trouver les énergies potentielle et cinétique, et donc le Lagrangien ^[ref] $\mathcal{L}$ correspondant:
$$ \left . \begin{array}{r c l} E_c & = & \frac{1}{2}mv^2=\frac{1}{2}m\left(\sqrt{\dot{x}^2+\dot{y}^2+\dot{z}^2}\right)^2 \\ & = & \frac{1}{2}ml^2\dot{\theta}^2\\ \\ E_p & = & -\vec{P}\cdot\vec{r}=mgz=-mgl\cos\theta\\ \\ \\ \mathcal{L} & = & E_c-E_p\\ & = & \frac{1}{2}ml^2\dot{\theta}^2+mgl\cos\theta\\ \end{array} \right . $$

Les équations d'Euler-Lagrange nous donnent alors, avec $\theta$ pour coordonnée généralisée: $$ \begin{eqnarray} \frac{\partial \mathcal{L}}{\partial \theta} = \frac{\text{d}}{\text{d}t}\frac{\partial \mathcal{L}}{\partial\dot{\theta}} \; & \Rightarrow \; & \ddot{\theta}=-\frac{g}{l}\sin\theta \end{eqnarray} $$

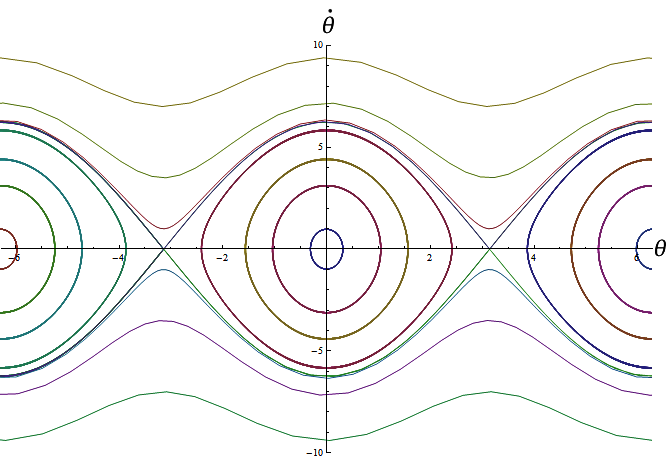
Trajectoire et portrait de phase

On va maintenant intégrer l'équation obtenue pour obtenir la trajectoire spatiale et le portrait de phase du pendule simple.
Le mouvement étant plan, la trajectoire est aisée à deviner: on obtiendra une portion de cercle.