Le nouveau pendule chaotique

Etude détaillée du pendule chaotique
Section de Poincaré

Pour caractériser le comportement de notre système, nous aurons besoin d'utiliser une section de Poincaré ^{[ref1] [ref2]}. Les sections de Poincaré sont des sous-espaces qui sont traversés par le système de manière récurrente et transverse.
Dans notre cas, la section de Poincaré choisie est une portion du plan $yOz$ qui, lorsqu'elle sera traversée, relèvera les valeurs de $\theta$ et $\dot{\theta}$.
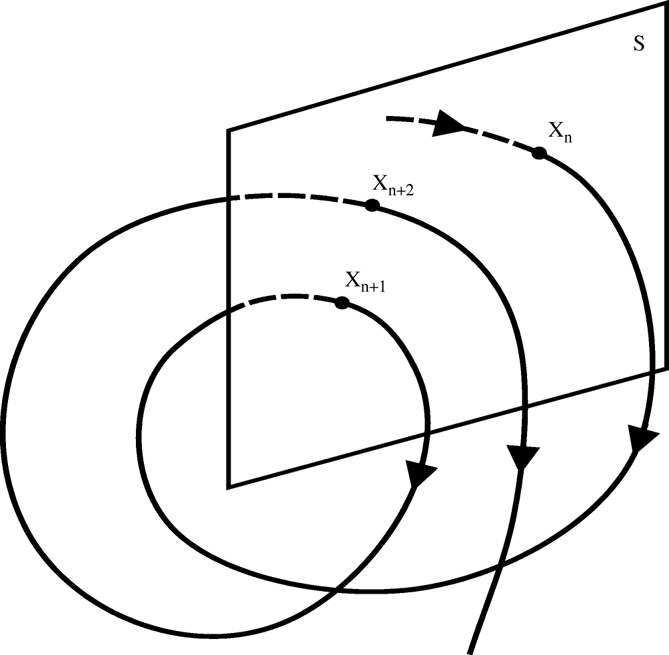On pourra, après avoir relevé un nombre conséquent de points, tracer le graphe de la section de Poincaré. Ce graphe peut être :

• un unique point: le système est périodique;
• un petit nombre de points: le système est périodique;
• une courbe fermée: le système est quasi-périodique;
• un nuage de points: le système est chaotique.

Voici quelques exemples de sections de Poincaré :

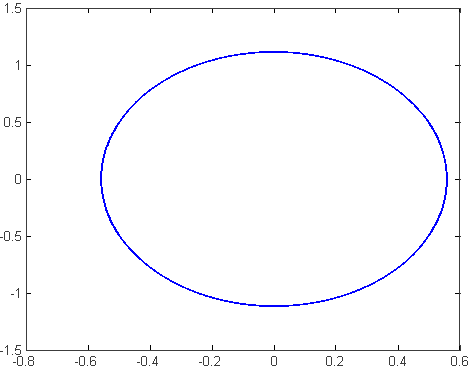Système quasi-périodique Image LASIN, uni-lj $[1]$	Système chaotique Image N. De Leon $[2]$

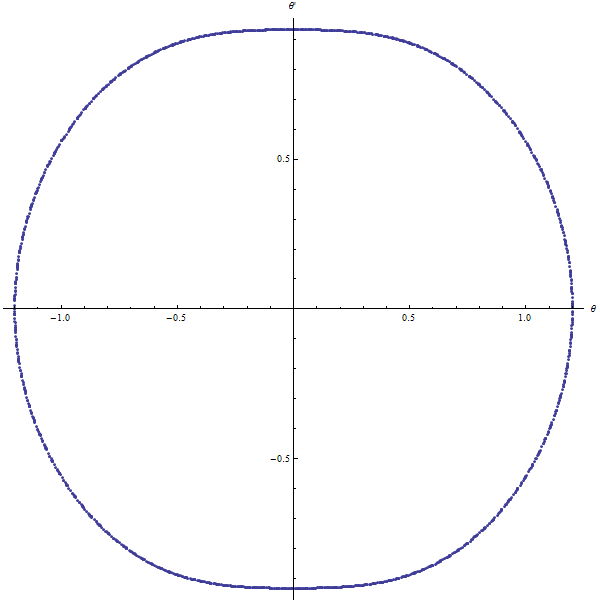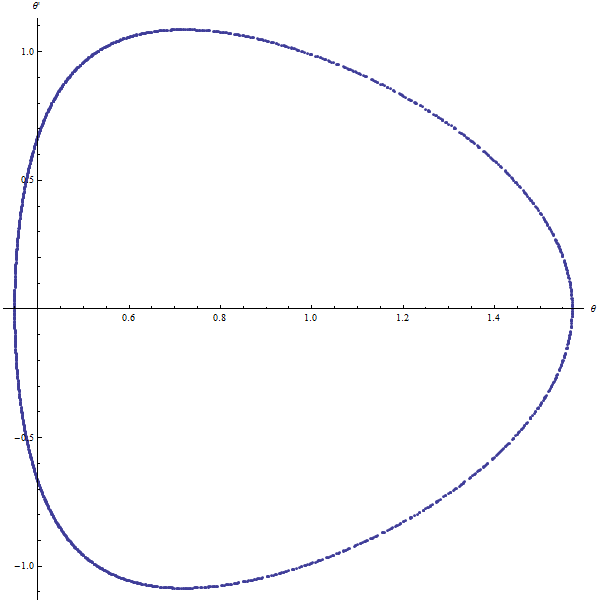pendule sphérique $(\alpha=0)$	Pendule sphérique

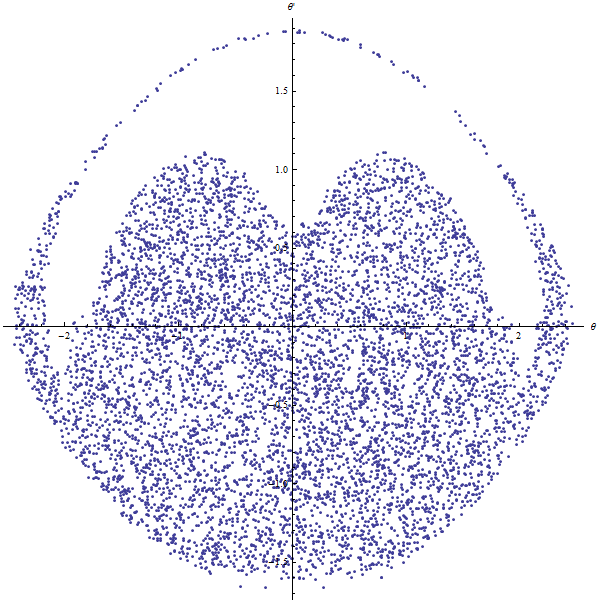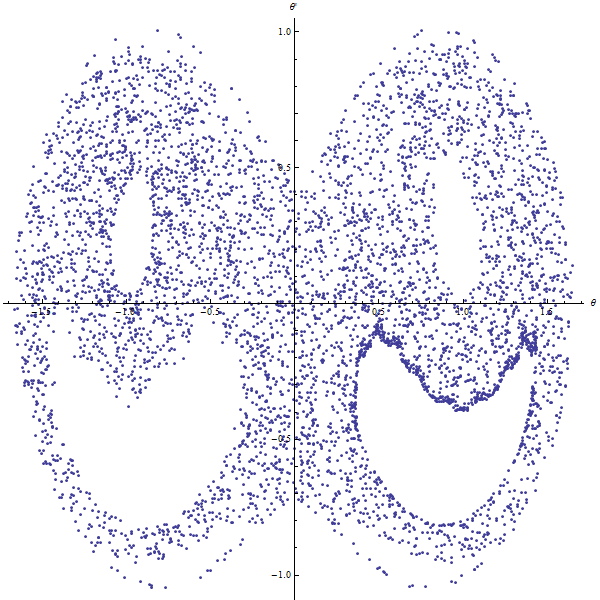pendule chaotique	pendule chaotique