Le nouveau pendule chaotique

Etude préliminaire – cas du pendule sphérique

On se penche maintenant sur le cas du pendule sphérique. On ajoute un degré de liberté au cas précédent: la masse peut tourner autour de l'axe $z$ en faisant un angle $\varphi$ avec l'axe $x$. Le mouvement se fera donc dans trois dimensions et non plus dans un plan.

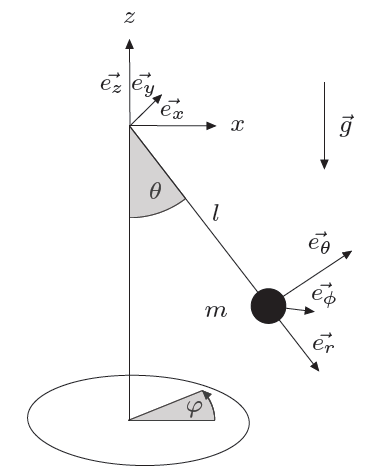
Positions et vitesses

Commençons par chercher les coordonnées de la masse en fonction des angles $\theta$ et $\varphi$, ainsi que les vitesses correspondantes: $$ \left \{ \begin{array}{r c l} x & = & l \sin \theta \cos \varphi \\ y & = & l \sin \theta \sin \varphi \\ z & = & -l \cos \theta \end{array} \right . \; \Rightarrow \; \left \{ \begin{array}{r c l} \dot{x} & = & l (\dot{\theta} \cos \theta \cos \varphi - \dot{\varphi} \sin \theta \sin \varphi ) \\ \dot{y} & = & l (\dot{\theta} \cos \theta \sin \varphi + \dot{\varphi} \sin \theta \cos \varphi )\\ \dot{z} & = & l \dot{\theta} \sin \theta \end{array} \right . $$

énergies, Lagrangien, équations du mouvement

On peut alors trouver les énergies potentielle et cinétique, et donc le Lagrangien $\mathcal{L}$ correspondant:
$$ \begin{eqnarray*} E_c & = & \frac{1}{2}m v^2=\frac{m}{2}(\dot{x}^2+\dot{y}^2+\dot{z}^2)=\frac{m l^2}{2}(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta) \\ E_p & = & -\vec{P}\cdot\vec{r}=mgz=-mgl\cos\theta \\ \\ \mathcal{L} & = & E_c - E_p = \frac{m l^2}{2}(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta) + mgl\cos\theta \end{eqnarray*}\\ $$ On en déduit les équations d'Euler-Lagrange: $$ \begin{eqnarray} \frac{\partial \mathcal{L}}{\partial \theta} = \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\theta}} \; & \Rightarrow \; & \ddot{\theta}=\dot{\varphi}^2\sin\theta\cos\theta-\frac{g}{l}\sin\theta \\ % \frac{\partial \mathcal{L}}{\partial \varphi} = \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\varphi}} \; & \Rightarrow \; & \ddot{\varphi}=-2\dot{\theta}\dot{\varphi}\cot\theta \end{eqnarray} $$

Intégration des équations

On peut maintenant intégrer numériquement les équations couplées obtenues plus haut (on se servira dans notre cas de Wolfram Mathematica 8 ).
Au final, on obtient les trajectoires suivantes, dépendant évidemment des conditions initiales imposées:

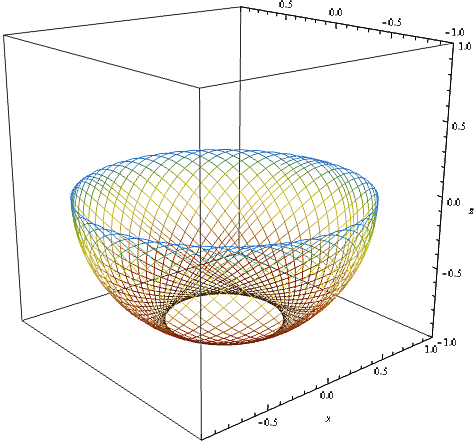
On remarque que la zone centrale n'est jamais atteinte par le pendule, et la forme en « bol » des trajectoires : le pendule décrit maintenant une portion de sphère.
Comme dans le cas du pendule simple, l'énergie mécanique est conservée, et l'énergie cinétique $E_c$ s'annule pour une même valeur de l'énergie potentielle $E_p$ - le pendule atteint alors une hauteur maximale et « retombe ».