Le nouveau pendule chaotique

étude détaillée du pendule chaotique
Étude de stabilité

Pour déterminer si un point fixe est stable ou instable, nous allons faire une étude de stabilité linéaire : on se place sur le point fixe, auquel on ajoute une petite perturbation. L'étude de la perturbatin nous renseignera sur la stabilité du point fixe.
Nous étudierons deux points fixes.

étude d'un premier point

On commence par s'intéresser au point $\theta = \alpha \; , \; \varphi = \frac{\pi}{2}$. On ajoute une perturbation : $\theta = \alpha + \theta _1\; , \; \varphi = \frac{\pi}{2} + \varphi _1 \;$, où $\theta _1 , \varphi _1 \ll 1$. Après simplification et linéarisation, on obtient :

$$\left \{ \begin{eqnarray*} \ddot{\theta _1} &=& -\theta _1 \\ % \ddot{\varphi _1} &=& -\frac{1}{1+\frac{\beta}{\sin ^2 \alpha}}\varphi _1 \end{eqnarray*} \right .$$

On reconnaît ici des équations d'oscillateurs harmoniques pour chaque variable – on peut donc en déduire que le point fixe est stable.

étude d'un second point

Étudions maintenant le cas du point $\theta = \pi , \varphi = 0$. En procédant de la même manière que pour le premier point, on trouve les équations suivantes :

$$\left \{ \begin{array}{r c l} \ddot{\theta _1}&=& \theta _1 \cos \alpha -\varphi _1 \sin \alpha \\ % \ddot{\varphi _1}&=& -\frac{\sin \alpha}{\beta} \theta _1 \end{array} \right .$$

On va cette fois-ci intégrer numériquement ces équations couplées et tracer les graphes de $\theta _1 (t)$ et $\varphi _1 (t)$ pour voir l'évolution des perturbations. On obtient ces deux courbes :

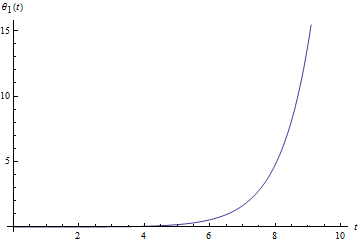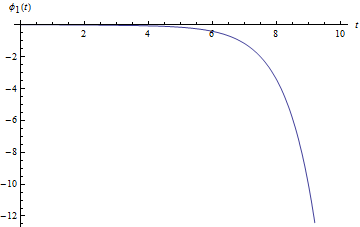Évolution de la perturbation $\theta _1 (t)$	Évolution de la perturbation $\varphi _1 (t)$

On voit bien que les deux perturbations divergent : ce point fixe est donc instable.