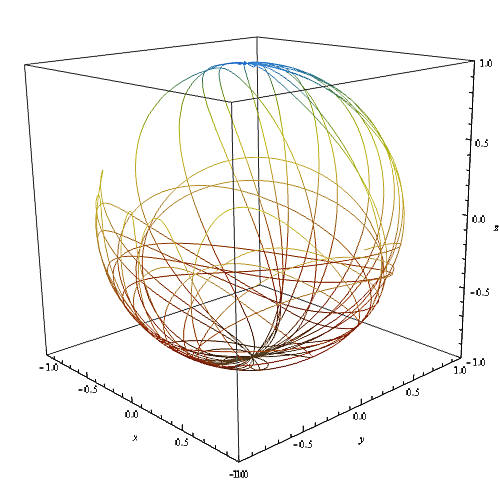
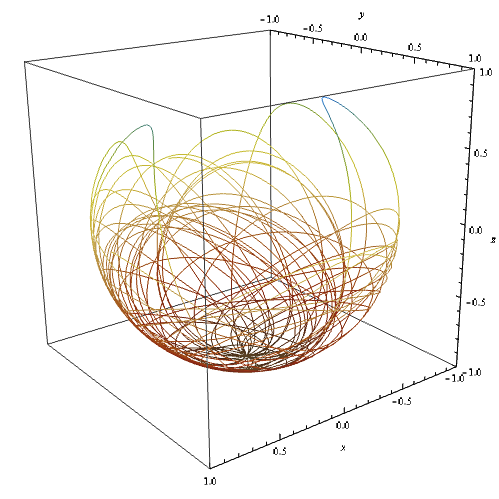
Le nouveau pendule chaotique

Etude préliminaire – cas du pendule chaotique

Pour pouvoir observer un comportement chaotique du pendule, on rajoute au cas précédent (pendule sphérique incliné) un disque rotatif de masse $M$ et de rayon $R$. Il faut également que l'angle $\alpha$ soit non nul.

énergie cinétique, Lagrangien, équations du mouvement

Dans le cas présent, la seule différence notable avec le cas précédent sera l'expression de l'énergie cinétique, à laquelle on rajoute un terme inertiel lié au disque : $$ \begin{eqnarray*} E_c & = & \frac{1}{2}ml^2(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta)+\frac{1}{2}MR^2\dot{\varphi}^2 \\ \\ % \mathcal{L} & = & \frac{1}{2}ml^2(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta)+\frac{1}{2}MR^2\dot{\varphi}^2 + mgl(\sin\theta\sin\varphi\sin\alpha+\cos\theta\cos\alpha) \end{eqnarray*} $$

On peut alors trouver les équations d'Euler-Lagrange du pendule chaotique : $$ \begin{eqnarray} \frac{\partial \mathcal{L}}{\partial \theta} & = & \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\theta}} \; \Rightarrow \; \ddot{\theta}=\dot{\varphi}^2\sin\theta\cos\theta+\frac{g}{l}(\cos\theta\sin\varphi\sin\alpha-\sin\theta\cos\alpha) \quad \qquad (1) \\ % \frac{\partial \mathcal{L}}{\partial \varphi} & = & \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\varphi}} \; \Rightarrow \; \ddot{\varphi}=\frac{ml\sin\theta(g\cos\varphi\sin\alpha-2l\dot{\theta}\dot{\varphi}\cos\theta)}{ml^2\sin^2\theta+MR^2} \qquad \qquad \qquad \qquad (2) \end{eqnarray} $$

intégration des équations

On intègre les dernières équations trouvées de la même manière que dans les cas précédents. Cette fois-ci, les trajectoires obtenues sont potentiellement chaotiques : on l'observera si les conditions initiales sont favorables.