The new chaotic pendulum

Preliminary study
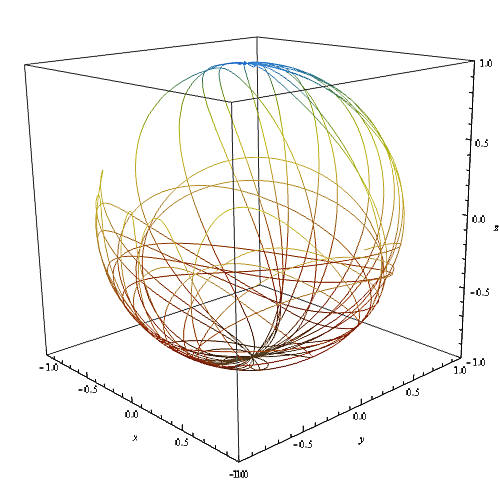
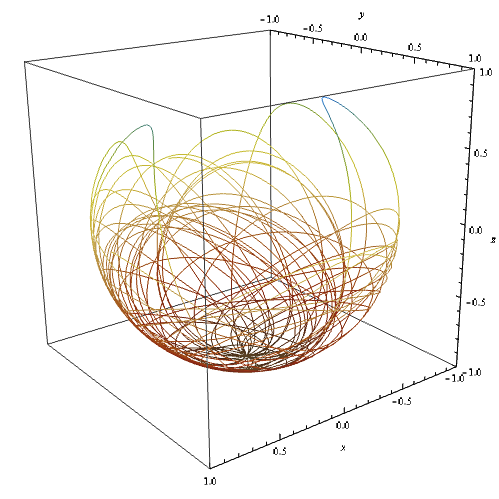
case of the chaotic pendulum

In order to observe a chaotic behaviour with our pendulum, we add to the previous case (the inclined spherical pendulum) a rotative disc with a mass $M$ and a radius $R$. We also want the angle $\alpha$ to be non zero.

Kinetic energy, Lagrangian, movement equations

In the current case, the only noticeable difference with the previous case will be the kinetic energy's expression, to which we add an inertial term from the disc : $$ \begin{eqnarray*} E_k & = & \frac{1}{2}ml^2(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta)+\frac{1}{2}MR^2\dot{\varphi}^2 \\ \\ % \mathcal{L} & = & \frac{1}{2}ml^2(\dot{\theta}^2+\dot{\varphi}^2\sin^2\theta)+\frac{1}{2}MR^2\dot{\varphi}^2 + mgl(\sin\theta\sin\varphi\sin\alpha+\cos\theta\cos\alpha) \end{eqnarray*} $$

We can now find the Euler-Lagrange equations for the chaotic pendulum : $$ \begin{eqnarray} \frac{\partial \mathcal{L}}{\partial \theta} & = & \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\theta}} \; \Rightarrow \; \ddot{\theta}=\dot{\varphi}^2\sin\theta\cos\theta+\frac{g}{l}(\cos\theta\sin\varphi\sin\alpha-\sin\theta\cos\alpha) \quad \qquad (1) \\ % \frac{\partial \mathcal{L}}{\partial \varphi} & = & \frac{\text{d}}{\text{d} t}\frac{\partial \mathcal{L}}{\partial\dot{\varphi}} \; \Rightarrow \; \ddot{\varphi}=\frac{ml\sin\theta(g\cos\varphi\sin\alpha-2l\dot{\theta}\dot{\varphi}\cos\theta)}{ml^2\sin^2\theta+MR^2} \qquad \qquad \qquad \qquad (2) \end{eqnarray} $$

integrating the equations

As we did previously, we integrate the latest equations. This time, the trajectories we get are potentially chaotic : we will see it if the initial conditions are favorable