Mise en pratique
Nous présentons ici le cheminement et les outils que nous avons utilisés afin de répondre aux objectifs que nous nous sommes posés.
1-Données
Les données que nous utilisons pour estimer les masses de nos deux amas se présentent sous un format commun. Nos catalogues de données contiennent :
- Les identifiants des objets dans la base de données source.
- Les positions des objets en coordonnées (Ascension Droite (RA), Déclinaison (DEC)) en dégrées.
- Les magnitudes apparentes de objets à travers différents filtres.
- Les décalages spectroscopiques.
Les deux amas ont des sources de données différentes, pour Abell 209 nous avons récupéré nos données sur le site de l'étude CLASH sur ce dernier on trouve deux catalogues, un contenant les données photométriques (magnitudes apparentes) et un second contenant les données spectroscopiques (décalages vers le rouge). Afin d'obtenir un catalogue unique contenant l’intégralité des données nous avons utilisé le logiciel TOPCAT permettant de faire correspondre les objets un à un, grâce à leurs positions dans le ciel.
Pour Coma n'ayant pas accès à un catalogue préexistant nous avons effectué une requête auprès du service de requête du Sloan Digital Sky Servey (SDSS). Nous avons alors demandé toutes les données photométriques et spectroscopiques dans un rayon de 85.2 minutes d'arc autour de la position de l'amas et ayant un décalage spectroscopique entre 0 et 0.05. Ce choix de requête ce base sur la literature, 85.2 minutes d'arc correspond à une taille de $~ 2.2Mpc$ autour de l'amas ce champ enveloppe donc le rayon viriel et nous permet d'étudier l'amas avec suffisamment de recul. Les limites sur le décalage sont, choisies grâce à la littérature, en effet l'amas de coma a fait l'objet de nombreuses études, toute ces dernières placent l'amas a un décalage vers le rouge cosmologique de de $z = 0.02$ notre choix englobe alors le centre de l'amas et sera suffisamment large pour comprendre les variations dus aux vitesses propres des galaxies membres, en prenant un maximum de dispersion de l'ordre de $1500 km\cdot s^{-1} ~ \sigma_{Zmax} = 0.005$
2-Estimation de la position de l'amas
La première chose que nous cherchons à définir est la position de l'amas dans l'espace des redshifts. Dans cette espace l'amas est caractérisé par une surdensité, Nous supposons cette distribution de redshifts comme étant gaussienne et nous choisissons le mode de cette distribution comme étant la position de l'amas. Pour obtenir une première approximation nous reportons tous les décalages vers le rouge du catalogue dans un histogramme dont nous prenons la position du maximum (le mode). Nous prenons alors autour de cette valeur tous les décalages compris dans un intervalle de $\pm 4\sigma_{Zmax}$ avec $\sigma_{Zmax}=\frac{\sigma_{Vmax}}{c}(1+z) $ avec le même choix $\sigma_{Vmax}=1500 km\cdot s{-1}$
A partir de cette sous partie du catalogue nous effectuons une étude plus poussée afin d'estimer avec plus de précision le positon de l'amas. Pour cela nous utilisons non plus le mode de l’histogramme car ce dernier est très sensible aux fluctuations statistiques et limiter par la taille des boites. Nous optons donc pour l'utilisation de la médiane car elle est moins sensible aux fluctuations statistiques que le mode et moins sensible aux dissymétries que la moyenne. La médiane est définie comme la valeur pour laquelle la distribution est séparée en deux échantillons de nombre égal. Dans le cas d'une distribution gaussienne la médiane et le mode sont confondus de ce fait dans l'hypothèse d'une distribution gaussienne il est raisonnable d'utiliser la médiane comme approximation du mode.
3-Transition entre redshifts et valeurs propres
Comme nous avons maintenant la position de l'amas dans l'espace des redshifts nous pouvons utiliser cette dernière afin de déterminer la vitesse propre de chaque objet. Pour cela nous faisons l'hypothèse que tous les membres de l'amas se trouvent tous à la même distance, la distance de l'amas. Nous calculons alors la vitesse propre associée à chaque galaxie grâce à la formule vue précédemment :
$$V_{p}=\frac{z_{v}-z_{cos}}{1+z}$$
Nous obtenons alors une nouvelle distribution, celle des vitesses propres radiales.
4-Test de Gaussienneté
Avant de procéder au calcul de la dispersion de vitesses radiale nous cherchons a vérifier une de nos hypothèse : La distribution est gaussienne.
Pour cela nous mettons un test d'Anderson Darling qui permet de juger si l'on peut rejeter ou non « l'hypothèse nulle », Si l'hypothèse nulle ne peut pas être rejetée alors il est probable que la distribution soit gaussienne et inversement si on peut la rejeter alors il est probable qu'elle ne le soit pas.
Nous utilisons pour cela le test d'Anderson Darling. Nous avons pour cela utilisé la méthode et les notions explicitées ici. De plus nous avons adapté le test pour plusieurs tailles d'échantillons à l'aide du tableau des valeurs critiques suivant :
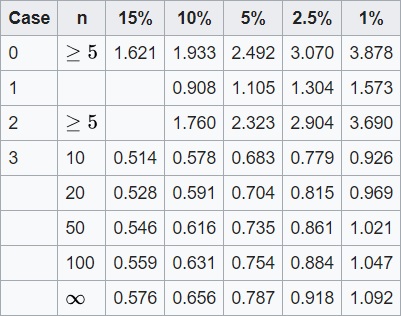
5-Dispersion des Vitesses
A présent nous pouvons calculer une des valeurs qui nous permet d'estimer la masse de l'amas étudié, la dispersion de vitesse radiales. Pour cela nous utilisons un outil statistique permettant de calculer la variance d'une distribution tout en étant moins sensible aux fluctuations statistiques: le Bi-Weight Midvariance.
Le Bi-Weight Midvariance, que nous nommons par abus de langage Bi-Weight, est un outil basé sur le calcul de la médiane afin de donner une dispersion dans une distribution quelconque, robuste et plus efficace qu'un calcul standard, il permet notamment d'être moins sensible aux valeurs extrêmes.
$$\zeta_{bivar} = n \ \frac{\Sigma_{|u_i| < 1} (x_i - M)^2 (1 - u_i^2)^4} {(\Sigma_{|u_i| < 1} (1 - u_i^2) (1 - 5u_i^2))^2}$$
Où $x_i$ correspond aux valeurs des données et $M$ la médiane classique et $u_i$ est donné par la relation suivante :
$$u_{i} = \frac{(x_i - M)}{c * MAD}$$
Avec $c$ une constante de réglage et $MAD$ la deviation absolue sur la médiane (MAD en anglais).
La racine carrée du Bi-Weight et un bon estimateur de dispersion car plus robuste et plus efficace que l'écart type.
6-Estimation des Incertitudes
Il faut se rappeler que n'importe qu'elle mesure scientifique sans incertitudes a peu de valeur. Et que ses dernières permettent notamment de comparer les résultats obtenus par différentes équipes. A cet effet nous allons expliciter nos méthodes de calcul d’incertitude sur les résultats.
Avant de calculer l'erreur sur la masse nous revenons sur la dépendance de cette dernière sur les autres paramètres. En effet la masse dépend de deux paramètres la dispersion de vitesse et le rayon harmonique et de ce fait sont incertitude dépendra également de ces deux paramètres et de leurs incertitudes.
6.1-Erreur sur le Rayon Harmonique
L'erreur sur le rayon harmonique provient principalement de l’erreur sur la mesure de la position de chaque objet, les mesures de position étant très précise on choisit de négliger cette source d'erreur devant l'erreur sur la dispersion de vitesse.
Pour autant il existe aussi des biais liés au calcul de ce derniers, ces derniers étant dus à la présence de galaxies visiblement très proches dans l'amas ou couples de galaxies et à la présence de galaxies non membre de l'amas par exemple.
Il existe aussi une erreur de nature statistique qui dépend de l’échantillon étudier. Il existe des méthodes permettant de quantifier ses erreurs, notamment les méthodes « bootstrap » ou « jacknife » basées sur le principe de Monte Carlo. N'ayant pas le temps de mettre en place ces méthodes nous négligeront l'incertitude.
6.2-Erreur sur la Dispersion de Vitesse
Étant l'erreur qui aura le plus d'influence sur l'estimation de la masse de l'amas nous ne pouvons pas nous contenter de la négliger comme nous l'avons fait pour le rayon harmonique.
Nous considérons donc la précision sur la mesure d'un décalage vers le rouge, en effet la dispersion découle directement de ces mesures et donc devrait être influencée par l'erreur sur ces dernières. Si on étudie le procédé que nous utilisons afin d'obtenir la dispersion, nous reportons des mesures de décalage dans un histogramme. En soit, nous construisons un ensemble de pics de hauteur variable en comptant le nombre d'objets qui se trouvent entres les deux bornes de la case ou « bin » en anglais. Pour autant, chaque objets possèdent une incertitude ce qui peut induire un débordement sur plusieurs bins à la fois. En interprétant l'incertitude comme la largeur d'une petite gaussienne se trouvant à l’emplacement de l'objet, ceci aura donc pour effet d'élargir la distribution finale et donc aura une influence sur la mesure de la dispersion, donnant donc lieu à une erreur systématique sur la mesure de dispersion. Pour se débarrasser de ce biais lié à l’imprécision des instruments il faudrait effectuer une déconvolution, c'est a dire retirer toutes les petites gaussiennes liées à chaque point pour se retrouver avec une distribution de pics de Dirac ayant une position ponctuelle qui sera plus représentative de la distribution réelle des décalages vers le rouge. N'ayant encore pas le temps de mettre en place de tels procédés nous négligeons seulement cet effet car cela a une faible influence par rapport à l'erreur statistique.
L'erreur statistique prédomine fortement sur cette mesure et afin de l'estimer rigoureusement il faudrait avoir recours à des méthodes du type Monte Carlo. Comme nous n'avons pas le temps de les mettre en place nous nous contenteront d'un calcul d’erreur standard sur une mesure de dispersion.
Pour un échantillon d'une taille supérieur a 10 il est raisonnable d'utiliser approximation :
$$\frac{\Delta\sigma}{\sigma}\approx \frac{1}{\sqrt{2(n-1)}}$$
Cette première approximation permettra une de donné un ordre de grandeur aux incertitudes même si elles sont grandement sous estimées.
6.3-Erreur sur la Masse
Il suffit à présent de propager l'erreur sur la masse :
$$\Delta M= \sqrt{\left( \frac{\partial M}{\partial\sigma_{v}}\right )^2(\Delta \sigma_{v})^{2} +\left( \frac{\partial M}{\partial R_{PW}}\right )^2 (\Delta R_{PW})^2}$$
Ce qui revient dans notre cadre à :
$$\Delta M=\frac{\partial M}{\partial\sigma_{v}}\Delta \sigma_{v}$$
$$\Delta M=\frac{3\pi}{G}2\sigma_{v}\Delta \sigma_{v}$$
D'où :
$$\frac{\Delta M}{M}=2\frac{\Delta\sigma_{v}}{\sigma_{v}}$$
Nous avons alors une estimation rapide de l'erreur sur la mesure. Rappelons une dernière fois que cette approximation lisse un grand nombre de problématique qui aurai étais intéressant de traiter avec plus de rigueur afin d'obtenir une incertitude à la fois représentative et robuste.