Comment Estimer la masse des amas de galaxies?
1- Les Méthodes
Il existe de nombreuses méthodes afin de déterminer la masse des amas de galaxies. Premièrement nous avons la méthode par les galaxies : elle consiste à appliquer le théorème du viriel sur les galaxies membres de l'amas. Deuxièmement, nous pouvons remonter à la masse à l'aide du Flux en Rayon X, en effet les nuages de gaz au sein de l'amas sont chauffés et émettent un rayonnement qui va alors traduire des phénomènes physiques bien particulier qui vont pouvoir être mis en évidence à l'aide de la spectroscopie. Troisièmement, le lentillage gravitationnel, phénomène physique à caractère gravitationnel, nous permet aussi de remonter de plusieurs façons à la masse de l'amas par l'observation de déformation de rayons lumineux dûe aux forts potentiels gravitationnels, dans certaines configurations particulières. D'autres méthodes comme celle de l'effet Sunyaev-Zel'dovich ou encore la méthode par la fonction de luminosité de l'amas sont aussi utilisés mais nous ne les traiteront pas ici par manque de temps. Nous nous concentrerons ici théoriquement, sur les 3 premières méthodes et nous appliquerons dans ce projet, la 1ère méthode qui est celle de la détermination de la masse des amas de galaxies à l'aide du théorème du viriel.
2- Hypothèses de travail
L'étude des amas de galaxies peut devenir très complexe dû à leur composition et leur dynamique complexe. Afin de pouvoir étudier de tels systèmes, nous allons effectuer des hypothèses qui auront pour but de simplifier le problème tout en essayant de garder une certaine cohérence avec les observations. Nous posons en ce sens les conditions d'un amas idéal.
Nous énonçons d'abord les hypothèses générales:
- L'amas a une symétrie sphérique.
- L'amas est un système fermé.
Pour l'étude à l'aide des galaxies nous faisons les hypothèses suivantes
- L'amas est un système autogravitant.
- L'amas est à l'équilibre dynamique.
- Les galaxies ont toutes la même masse.
- La distribution des vitesses des galaxies est isotrope.
Par autogravitant nous entendons que les forces gravitationnelles d’un corps sur les autres corps permettent à elles seules de maintenir le système dans une cohésion gravitationnelle pouvant être assimilé à un équilibre. Et finalement pour étudier l'amas grâce aux emisions en rayon X Nous supposons que:
- Le gaz est à l'équilibre thermodynamique et hydrostatique.
- Le gaz est soumis uniquement au potentiel gravitationnel de l'amas.
- Le gaz peut être assimilé à un gaz parfait.
3- Masse par les galaxies
Nous nous intéressons à la dynamique des galaxies à l'intérieur de l’amas, nous allons utiliser la dispersion des vitesses radiales des galaxies afin d’en déduire la masse totale de l’amas de galaxies. Pour ce faire nous utiliserons les hypothèses précédemment explicitées. Nous allons tenter de justifier l’hypothèse de l’amas considéré comme étant un système virialisé possédant la caractéristique d’être auto-gravitant. Pour cela nous avons besoin d’introduire le temps caractéristique de relaxation dynamique de notre amas, celui-ci correspond au temps qu’il faut à l’amas pour être à l’équilibre. Nous approximons ce dernier au temps nécessaire à une galaxie pour traverser l’amas en prenant une dispersion de $ \sim1000 km\cdot s^{-1}$ l'ordre de grandeur de l'écart à la loi de hubble observé que l'on utilise comme limite à la vitesse des galaxies. Nous remarquons que qu’il lui faut environ $1.5\times10^9$ ans pour traverser, ce qui est inférieur à l’âge de l’Univers que l'on considère comme étant de l'ordre de grandeur de la durée de vie d'un amas. Nous pouvons donc conclure que les galaxies ont la possibilité de faire plusieurs orbites autour de l'amas et de ce fait, les amas de galaxies peuvent être à l'équilibre virialisé. Nous pouvons donc appliquer le théorème du viriel à notre amas de galaxies.
$$2E_{kin}+E_{pot} = 0$$
$$E_{kin} = \frac{1}{2}\sum_{i}m_{i}v_{i}^{2}\; , \;E_{pot} = -\frac{1}{2}\sum_{i\neq j} \frac{Gm_{i}m_{j}}{r_{ij}}$$
Où $E_{kin}$ correspond à l’énergie cinétique de l’amas de galaxie et $E_pot$ à son énergie potentielle et $m_i$ et $v_i$, la masse de la i-ème galaxie de l’amas. Nous pouvons donc dans un premier temps approximer la masse de l’amas comme étant la somme des masses des galaxies qui le composent. C’est donc de cette façon que nous définirons la masse $m_i$ dans nos équations. Il est de plus important de définir la dispersion de vitesse comme étant :
$$\left \langle v^{2} \right \rangle := \frac{1}{M}\sum_{i}m_{i}v_{i}^{2}$$
Il faut aussi définir une limite à notre amas, pour cela nous allons prendre un rayon que nous allons appeler rayon gravitationnel, aussi appellé rayon viriel, définit de la façon suivante :
$$r_{G}:= 2M^{2}\left ( \sum_{i\neq j}\frac{m_{i}m_{j}}{r_{ij}} \right )^{-1}$$
Les équations d’énergie cinétique et potentielle peuvent donc s’écrire en fonction des variables explicitées précedement de la façon suivante :
$$E_{kin}= \frac{M}{2}\left \langle v^{2} \right \rangle\; , \;E_{pot}= -\frac{GM^{2}}{r_{G}}$$
Après application du théorème de Viriel, nous arrivons à l’équation de la masse de l’amas :
$$M = \frac{r_{G}\left \langle v^{2} \right \rangle}{G}$$
Cette détermination est bien sûr effectuée grâce à l’étude de notre système dans l’approximation d’une symétrie sphérique et donc utilisant la distance tri-dimensionnelle au centre de l’amas qui n’est pas directement observable. Afin d’appliquer cette méthode aux observations qui sont effectuées, on a besoin de projeter ces distances. Comme nous faisons l'hypothèse que la position et la direction des vecteurs vitesses des galaxies ne sont pas corrélés, soit une distribution isotropique des vitesses, cela nous donne :
$$\left \langle v^{2} \right \rangle = 3\sigma_{v}^{2}\; ,\; r_{G} = \frac{\pi}{2}R_{G}$$
$$R_{G} = 2M^{2}\left ( \sum_{i\neq j}\frac{m_{i}m_{j}}{R_{ij}} \right )^{-1}$$
Où $R_{ij}$ correspond à la séparation projeté entre la i-ème et j-ème galaxie. Le paramètre $\sigma_v$ et $R_G$ sont, quant à eux directement observables. Nous en déduisons donc la masse totale de l’amas :
$M=\frac{3\pi R_G \sigma^{2}_{v}}{2G}=1.1\times10^{15}M_\odot\left(\frac{\sigma_v}{1000 km\cdot s^{-1}}\right)^2\left(\frac{R_G}{1Mpc}\right)$
Nous remarquons que la masse totale de l’amas ne dépend plus des masses des galaxies qui le composent. Pour servir d’exemple on peut prendre le sigma v typique d’un amas de galaxie correspondant à 1000 km/s et le diamètre $R_G$ moyen de 1 Mpc nous donnant une masse moyenne de $10^{15}$ masse solaire correspondant à la masse d’un amas riche en galaxie.
4- Masse par le Gaz
Un des moyens d’étudier la dynamique du gaz est d’observer la façon dont il émet en longueur d’onde X. Comme présenté lors de l’introduction, pour des amas de galaxies ayant des masses entre $10^{13}$ et $10^{15}$ masse solaire, le gaz peut être chauffé à des températures allant de $10^7$ à $10^8$ K. A ces températures on ne plus réellement parler de gaz mais plutôt de plasma. Dans ce milieu la matière est constituée d'électrons libres et d'ions qui se réduisent presque à leurs noyaux.
Cette nature très particulière lui donne une signature spectrale unique. Le spectre d’émission du gaz résulte de la superposition de plusieurs mécanismes : Les raies d'émission des ions et le bremsstrahlung thermique (littéralement le rayonnement de freinage) qui génère un continuum d’émission. Le bremsstrahlung est produit lorsque deux particules chargées entrent en interaction, par exemple lorsqu’un électron passe à proximité d’un proton. L’interaction a pour effet de dévier les particules, cependant pour des raisons de conservation d’énergie, des photons sont émis. Due à l’agitation thermique, les électrons rencontrent en permanence les ions : la version thermique du phénomène précédent se produit. On peut donc grâce à cela remonter à une mesure de la température du gaz à l'intérieur de l’amas. On veut alors relier la température du gaz à la masse de l’amas. C’est à partir de cet instant que l’hypothèse du gaz à l’équilibre hydrostatique, distribué de façon sphérique devient pertinente. Pour justifier cette approximation on souhaite étudier la vitesse du son à l'intérieur de l’amas :
$$c_{s} = \sqrt{\frac{P}{\rho_{g}}} = \sqrt{\frac{nk_{B}T}{\rho_{g}}} = \sqrt{\frac{k_{B}T}{\mu m_{p}}} = 1000 km.s^{-1}$$
Avec P la pression du gaz, n la densité numérique du gaz,$\rho _g$ sa masse volumique, $\mu$ la masse moléculaire moyenne définie comme $\mu := \frac{\left \langle m \right \rangle}{m_p}$ avec $m_p$ la masse du proton. On regarde alors le temps nécessaire pour qu’une onde traverse un amas en prenant un rayon moyen. $t=\frac{2R_A}{c}\sim 7\times10^8 yr$ en supposant que la durée de vie d’un amas est supérieur à l’âge de l’univers $T\approx13.8\times10^9 yr$ on remarque que $t\ll T$et on en déduit que l’amas a le temps de se mettre à l’équilibre hydrostatique.
On peut alors utiliser la loi de l’hydrostatique : $\vec{\nabla}\left(P\right)=-g\vec{\nabla}\left( \Phi \right)$ où est le potentiel gravitationnel dans lequel repose le gaz. Il est intéressant de noter que le potentiel n’est pas définis seulement pour le gaz mais contient aussi toute la masse des galaxies et surtout celle de la matière noire, cette méthode permet donc de remonter jusqu’à la masse totale de l’amas. Pour résoudre cette équation nous faisons appel à la symétrie sphérique de l'amas parfait qui nous permet d'écrire.
$$\frac{1}{\rho _{g}}\frac{dP}{dr} = - \frac{d\Phi }{dr} = -\frac{GM(r)}{r^{2}}$$
Où M(r) est la masse inclus dans la sphère de rayon r. Nous insérons alors $P = nk_{B}T$ , hypothèse du gaz parfait. Nous obtenons alors l'expression
$$M(r) = -\frac{k_{B}T r^{2}}{G\mu m_{p}}\left (\frac{d\ln\rho_{g}}{dr} + \frac{d\ln T}{dr} \right ) $$
Nous remarquons que la masse de l'amas contenus à l'intérieur d'un rayon r s'exprime simplement en fonction du gradient de masse volumique, que nous pouvons obtenir à partir de la brillance de la source, et du gradient de température qui lui aussi est directement observable.
5- Masse par Lentillage Gravitationnel
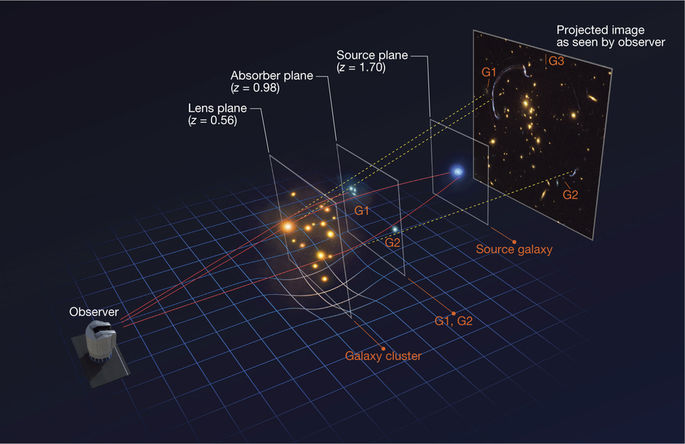
Nous nous intéressons a un dernier phénomène celui du lentillage gravitationnel prédit par la relativité générale d'Einstein. Le lentillage gravitationnel est la déviation de la lumière produite par la présence d'un corps massif situé entre l'observateur et la source émettrice. Ce phénomène a été observé pour la première en 1919 lors d'une l'éclipse totale de Soleil, et en 1979 avec des galaxies. Il existe deux types de lentillage gravitationnelle : le lentillage fort et faible. Le lentillage fort, comme nous le montre la figure, se traduit par une déformation annulaire de la lumière incidente d'une galaxie située derrière l'amas. Le lentillage fort se produit lorsqu'un alignement particulier entre l'observateur, la masse déviante et la galaxie d'arrière-plan s'effectue, il faut qu'il y ait aussi une distance relative particulière entre les objets ainsi qu'un objet déviant suffisamment massif pour provoquer le lentillage fort. La formation d'arcs de cercle est donc un phénomène localisé dans la zone où se situe la plus grande concentration de matière, c'est à dire le centre de l'amas. Connaissant la distance de la source déformée, celle de l'amas ainsi que la géométrie de l'arc, on peut donc remonter à la masse comprise au sein de la région définie par l'arc de cercle.
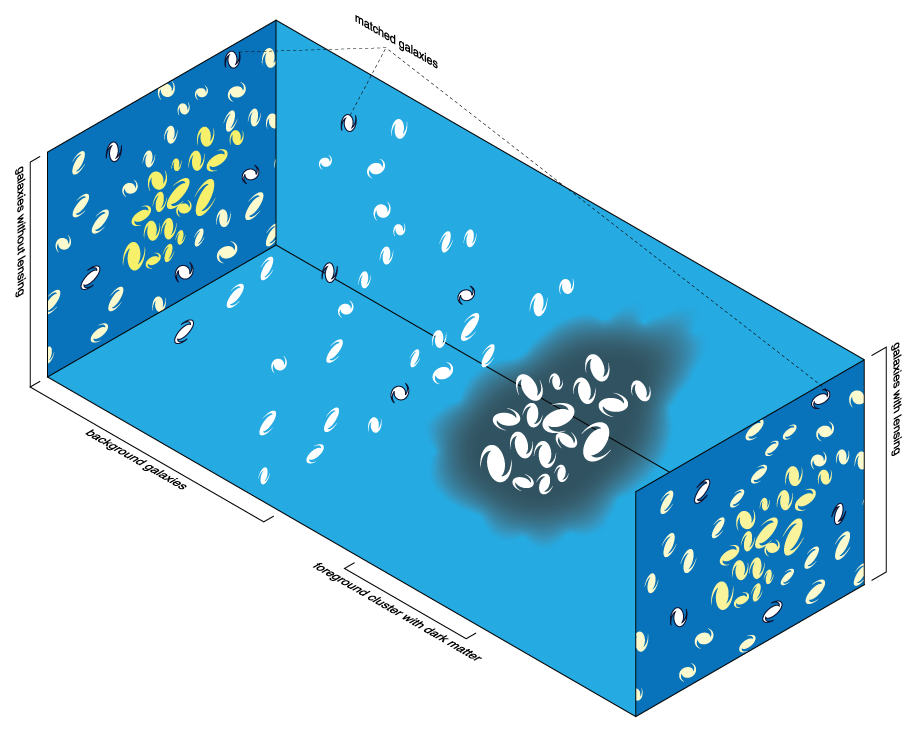
Afin d'accéder à la masse totale de l'amas, nous utilisons le lentillage gravitationnel faible. Ce phénomène, comme nous le montre la figure ci-dessous, se traduit par une rotation des orientations apparentes des galaxies situées en arrière-plan tendant vers une orientation tangentielle aux lignes équipotentielles du champ gravitationnel entourant l'amas de galaxie centré sur le coeur de l'amas. Contrairement au lentillage fort, nous n'avons pas de déformations morphologiques de galaxies mais seulement une rotation d'orientations apparentes de galaxies autour de l'amas. A l'aide d'outils statistiques, nous pouvons déterminer la masse totale de l'amas de galaxie. Nous remarquons alors que ces deux méthodes sont complémentaires l'une et l'autre, le lentillage fort, traduit un effet au centre, situé sur une région centrale de notre amas, là où la matière est majoritairement concentrée. Tandis qu'à l'opposé, le lentillage faible nous permet d'avoir une bonne approximation de la masse totale de l'amas en mettant en exergue une méthode statistique.