1- Résultats
Maintenant que nous avons un programme capable d'estimer la masse d'un amas de galaxies, nous décidons de comparer les résultats obtenus aux résultats de la littérature.
A cet effet nous cherchons des papiers qui traitent les mêmes amas que les nôtres.
1.1- Abell 209
Mercurio et al. 2003 obtiennent les résultats suivants reporté dans le tableau ci-dessous. Il est important de noter que l'auteur utilise une cosmologie différente et donc pour compenser la différence de cosmologie, il a fallu diviser tous les résultat par 0.7 afin d'être dans la même cosmologie. En effet la définition des distances entre deux objets dépend de la cosmologie utilisée et donc par extension de la masse. De plus nous possédons des données d'objets peu lumineux que n'avaient pas ces auteurs à l'époque. De ce fait on impose une coupure en magnitude à 21 afin d'avoir un échantillon comparable.
$$M_{vir}\; (\times 10^{15} M_{\odot})$$ |
$$\sigma_{v}\;(km\cdot s^{-1})$$ |
$$R_{vir}\; (Mpc)$$ |
|
| Mercurio et al. 2003 | $$3.22^{+0.92}_{-0.90}$$ |
$$1394^{+88}_{-99}$$ |
$$2.4$$ |
| Drevon et Richardson 2018 | $$3.86\pm 0.50$$ |
$$1278\pm 85$$ |
$$2.15$$ |
Nous remarquons que nos résultats sont cohérents avec ceux de Mercurio et al.
Nous comparons maintenant nos résultats avec Umetsu et al. 2016 qui mesure la masse de l'amas par lentillage gravitationnel faible. Il faut noter que le lentillage gravitationnel faible ne permet pas d’accéder aux mêmes grandeurs. Ici nous citons la valeur $M_{200c}$ qui correspond à la masse contenue dans le rayon $R_{200c}$ ce dernier est défini par rapport à la densité critique de l'univers, ce rayon correspond à un rayon pour lequel la densité est deux cents fois plus grande que dans le reste du ciel.
$$M_{200c}\; (\times 10^{15} M_{\odot})$$ |
$$\sigma_{v}\;(km\cdot s^{-1})$$ |
$$R_{200c}\; (Mpc)$$ |
|
| Umetsu et al. 2016 | $$1.540\pm 0.342$$ |
$$0.84\pm0.22$$ |
$$M_{vir}\; (\times 10^{15} M_{\odot})$$ |
$$\sigma_{v}\;(km\cdot s^{-1})$$ |
$$R_{vir}\; (Mpc)$$ |
|
Drevon et Richardson 2018 |
$$3.67\pm 0.20$$ |
$$1233\pm 35$$ |
$$2.19$$ |
On remarque que même si nos mesures ne sont pas faites dans le même rayon, le fait qu'avec un rayon plus large nous obtenons une masse plus grande nous permet de dire que nos mesures sont en accord. Ce même papier propose une masse viriel tri-dimensionelle pour l'amas. $M_{vir}^{a}=(1.960\pm 0.461) \times 10^{15}\; M_{\odot}$ Il est important de noter que cette masse est tridimensionnelle il faudrait donc la projeter et ensuite vérifier la définition de la masse viriel afin de comparer avec nos résultats.
Paulin-Henriksson et al. effectue en 2007 une étude sur cet amas grâce au lentillage gravitationnel faible. Dans leur étude ils convertissent leur résultat afin de pouvoir comparer ces dernier aux études dynamiques. Pour cela ils utilisent la définition : $$M(< R)=\frac{2}{G}\; \sigma_{v}^{2}\; R$$ on voit que cette définition diffèrent de la nôtre d'un facteur $\frac{3\pi}{2}$ en rétablissant ce facteur nous pouvons comparer nos mesures.
$$M_{vir}\; (\times 10^{15} M_{\odot})$$ |
$$\sigma_{v}\;(km\cdot s^{-1})$$ |
$$R_{vir}\; (Mpc)$$ |
|
| Paulin-Henriksson et al. 2007 | $$3.63 (1.8\frac{\; 3\pi}{2})$$ |
$$924\pm 84$$ |
$$1.8$$ |
| Drevon et Richardson 2018 | $$3.67\pm 0.20$$ |
$$1233\pm 35$$ |
$$2.20$$ |
Nous remarquons que les masses corrèlent bien entre elles, cependant les paramètres annexes présents au sein du tableau ne sont, eux, pas corrélés. En effet a l’intérieur du facteur multiplicatif que nous appliquons à la masse on effectue en quelque sorte un lissage sur tous les effets de projection et de divergence entre les définitions. De ce fait on ne peut pas estimer le facteur qu'il faudrait appliquer aux paramètres seuls. Mais nous pouvons cependant affirmer que nos masses sont en accord.
1.2- L'amas de Coma
Nous comparons alors les résultats obtenus pour Coma à ceux de la littérature.
Rines et al. 2003 estime la masse de plusieurs amas par une méthode comparable à la nôtre. Nous reportons alors nos résultats respectifs dans un tableau après avoir établi les résultats dans notre cosmologie.
$$M_{vir}\; (\times 10^{15} M_{\odot})$$ |
$$\sigma_{v}\;(km\cdot s^{-1})$$ |
$$R_{vir}\; (Mpc)$$ |
|
| Rines et al. 2003 | $$1.566 \pm 0.087$$ |
$$924\pm 84$$ |
$$2.14$$ |
| Drevon et Richardson 2018 | $$2.00\pm 0.15$$ |
$$973\pm 35$$ |
$$1.92$$ |
Nous remarquons que nos résultats sont proches à celle de la bibliographie mais qu'ils ne sont pas pour autant en accord parfait. Ceci peut être la conséquence de plusieurs facteurs : une différence dans les données utilisées ou bien une difference dans la définition de la masse viriel.
Kubo et al. 2007, estiment la masse de l'amas de coma à l'aide du lentillage gravitationnel faible. Après avoir rétablis les résultats dans notre choix de cosmologie nous les reportons dans le tableau suivant.
Chiu et al. (2018), nous apprend à passer de $M_{200}$ a $M_{vir}$ $$M_{vir}=0.88\; M_{200}$$
$M_{200}\; (\times 10^{15} M_{\odot})$ |
$\sigma_{v}\;(km\cdot s^{-1})$ |
$r_{200}\; Mpc$ |
|
| Kubo et al. 2007 | $2.69^{0.93}_{0.80}$ |
$2.84^{0.30}_{0.31}$ |
|
$M_{vir}\; (\times 10^{15} M_{\odot})$ |
$\sigma_{v}\;(km\cdot s^{-1})$ |
$R_{vir}\; (Mpc)$ |
|
| Kubo et al. 2007 | $2.36^{0.82}_{0.70}$ |
||
| Drevon et Richardson 2018 | $2.00\pm 0.15$ |
$973\pm 35$ |
$1.92$ |
Nous remarquons ici que même si les mesures présentées ne sont pas prise dans le même rayon, le rayons pris pour nos mesure étant plus petit nous remarquons en effet que la masse est plus faible. Dès lors nous pouvons affirmer que les deux mesures sont cohérentes.
2-Discussion
Tout au long de l'étude nous avons fait un certain nombre de choix et d'hypothèse, dans cette partie nous allons discuter de ces hypothèses est illustrer les certains choix.
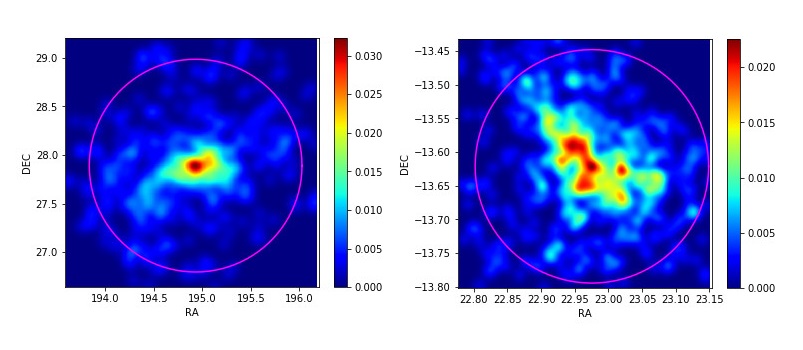
Attardons nous d'abord sur la symétrie supposée sphérique. Cette hypothèse et une de celle qui a permis de conduire à bout le raisonnement mais est elle réellement justifié ? En observant les cartes de densité produite par notre programme nous pouvons observer que pour Coma l'approximation d'une symétrie sphérique, du moins de ce que l'on voit sur la projection, semble justifié. Pour Abell 209 la densité projetée est loin d'être sphérique, en effet on voit apparaître une grande quantité de sous structures lorsque le lissage s’opère a une échelle de 100 kpc. En effet en lissant la littérature Mecurio et al. 2003 émettent l'hypothèse qu' Abell 209 serait en réalité trois amas étant dans un stade avancé de fusion.
2.1- Influence de la couleur
Nous avons aussi fait le choix de ne garder que les galaxies rouge lors du calcul de la masse. Ce choix étant justifié à la fois par la littérature (Saro et al. 2018) et par l'évolution des galaxies au sein de l'amas. Afin de s’assurer que notre choix est justifié nous nous proposons de faire une étude de l'influence de ces galaxies. Pour cela nous allons faire tourner une première fois le programme en gardant la séquence rouge, une seconde fois en gardant tout échantillon et une dernière fois en gardant uniquement la séquence bleue. De plus nous forcerons le programme a prendre le même rayon viriel pour les trois études afin d'obtenir des résultats comparables.
Nous commençons avec Abell 209, Le rayon viriel que nous utilisons est:
$$R_{vir}=2.20 Mpc $$
$M_{vir}\; (10^{15} M_{\odot})$ |
$\sigma_{v}\; (km\cdot s^{-1})$ |
|
| Les rouges | $3.67 \pm 0.20$ |
$1233\pm 35$ |
| Tous ensemble | $5.10\pm 0.25$ |
$1455\pm 35$ |
| Les bleues | $9.93\pm 0.95$ |
$2029\pm 95$ |
nous poursuivons alors avec l'amas de Coma pour ce dernier le rayon viriel est fixé à
$$R_{vir}=1.92 Mpc $$
$M_{vir}\; (10^{15} M_{\odot})$ |
$\sigma_{v}\; (km\cdot s^{-1})$ |
|
| Les rouges | $2.00 \pm 0.15$ |
$973\pm 35$ |
| Tous ensemble | $2.30\pm 0.15$ |
$1046\pm 30$ |
| Les bleues | $4.31\pm 0.75$ |
$1430\pm 150$ |
On remarque en effet que le fait d’inclure ou non les galaxies bleues a pour influence de sur estimer la masse de l'amas. Cela étant dû au fait que les galaxies bleues étant arrivée plus récemment dans l'amas ont une « mémoire » de leur dynamique en dehors de l'amas, Ce qui fait que leur vitesse n'est pas représentative de du potentiel de l'amas, ce qui aura pour effet d'élargir la distribution.
2.2- Influence de le la magnitude
Nous choisissons maintenant d'effectuer une petite étude sur l'influence d'une coupure en magnitude sur l'estimation. En effet afin de pouvoir comparer nos mesures pour Abell 209 avecMecurio et al. 2003 nous avons coupé notre échantillon afin d'avoir un échantillon similaire à celui utiliser dans l'étude. Ici nous proposons plusieurs mesures sur Abell 209 avec diverse coupure en magnitude apparente. Afin de pouvoir comparer les résultats nous fixons le rayon viriel à la valeur obtenus lorsque nous ne coupons pas les données soit : $R_{vir}=2.20\; Mpc$.
$M_{vir}\; (10^{15} M_{\odot})$ |
$\sigma_{v}\; (km\cdot s^{-1})$ |
|
| Sans coupure | $3.67 \pm 0.20$ |
$1233\pm 35$ |
| m< 21 | $4.14\pm 0.55$ |
$1310\pm 88$ |
| m< 22 | $3.61\pm 0.30$ |
$1224\pm 54$ |
| m< 23 | $3.41 \pm 0.25$ |
$1189\pm 40$ |
| m< 24 | $3.76\pm 0.20$ |
$1250\pm 36$ |
Nous reportons les résultats dans un graphique:
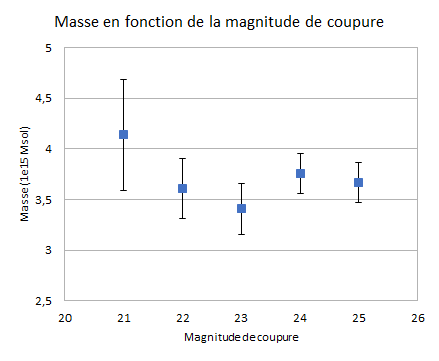
Nous remarquons en effet une certaine variation mais les barres d'erreur ne permettent pas d'écarter le fais que ces variations ne soit uniquement des fluctuations statistiques.
Nous calculons la magnitude apparente médiane $m_{med}=23.18$ et choisissons de regarder si les galaxies les plus brillantes respectivement moins brillantes sont plus représentative du potentiel de l'amas que les galaxies moins brillantes respectivement plus brillantes. Nous effectuons toujours cet étude dans un rayon viriel de $R_{vir}=2.20\; Mpc$.
$M_{vir}\; (10^{15} M_{\odot})$ |
$\sigma_{v}\; (km\cdot s^{-1})$ |
|
| m< 23.18 | $4.07 \pm 0.40$ |
$1299\pm 61$ |
| m> 23.18 | $3.57\pm 0.25$ |
$1216\pm 40$ |
Nous remarquons en effet que les galaxies les plus faible donnent une estimation plus proche de l'estimation totale comparé aux galaxies les plus brillantes. Ceci semble logique lorsqu'on pense au fait que la majorité des galaxies les plus brillantes se trouvent au centre de l'amas, en ce lieu la concentration en galaxies est beaucoup plus forte et de ce fait les galaxies ont beaucoup plus de chance de se rencontrer et donc leurs dynamiques n'est plus uniquement celle du potentiel de l'amas et cela a donc un impact sur le résultat. Les galaxies moins brillantes se trouvent dans des régions beaucoup plus éloignées du centre de l'amas et de ce fait elles ont moins de chance d'interagir entre elle et tracerons mieux le potentiel de l'amas.
3- Résultats de la littérature originaux
Nous avons modifier les résultats de la littérature a plusieurs effet, rétablir la cosmologie choisie, passer d'un type de mesure à un autre ou encore rétablir le changement de définition dans cette section nous allons lister les résultat tels qu'il sont présentés dans la littérature
3.1- A209
Mercurio et al. 2003
$$M(< R_{vir})=2,25^{+0.63}_{-0.65} \times10^{15}\;h^{-1}M_{\odot} \;,\;\sigma_{v}=1394^{+88}_{-99}\;km\cdot s^{-1}\;,\;R_{vir}\sim 1.7h^{-1}Mpc$$
Umetsu et al. 2016
$$M_{200c}=1.540\pm0.342 \times10^{15}\;h^{-1}_{70}M_{\odot} \;,\;r_{-2}= 0.84h^{-1}_{70}Mpc$$
Paulin-Henriksson et al.
$$M_{200}=7.7^{+4.3}_{-2.7} \times10^{14}\;h^{-1}M_{\odot} \;,\;r_{200}= 1.81^{+0.30}_{-0.26}h^{-1}Mpc$$
3.2- Coma
Rines et al. 2003
$$M_{proj}=1,090\pm 0.061 \times10^{15}\;h^{-1}M_{\odot} \;,\;\sigma_{v}=957^{+30}_{-28}\;km\cdot s^{-1}\;,\;r_{200}= 1.5h^{-1}Mpc$$
Kubo et al. 2007
$$M_{200}=1.88^{+0.65}_{-0.56} \times10^{15}\;h^{-1}M_{\odot} \;,\;r_{200}= 1.99^{+0.21}_{-0.21}h^{-1}Mpc$$