Animations
| trajectories | Poincaré section | first return application |
distance to fixpoint |
curves φ(t) , φ'(t) , θ (t) , θ'(t) |
complete |
Animation 4
distance to fixpoint
This programs traces $\cos (\theta (t))+1$, representing the distance across time between the mass and the unstable fixpoint $\theta = \pi \; , \; \varphi = 0$ : this function's value is zero for $\theta = \pm \pi$ .
We observe that is we release the pendulum from the unstable fixpoint $\theta = \pi - \mid \alpha \mid \; , \; \varphi = \frac{\pi}{2}$ with the initial conditions given in the application below, we may see an inversion of the pendulum's rotating direction with respect to $\varphi$ , occuring when the pendulum passes by the unstable fixpoint $\theta = \pi \; , \; \varphi = 0$ .
In the present case, the value of $\varphi (t)$ does not change anything when $\theta=\pm\pi$. It is therefore not necessary to trace the curve of $[ \varphi (t), 2 \pi ]$
Here are some images if you can't see the program :
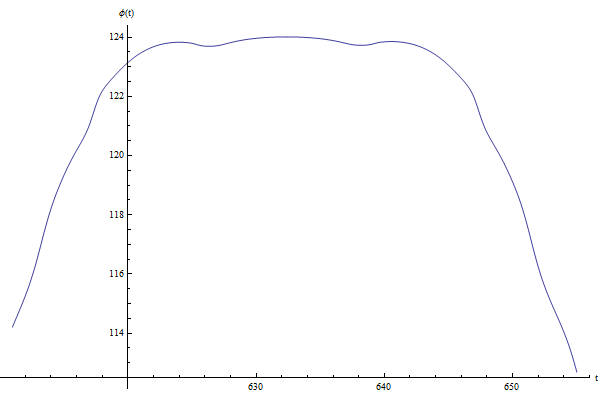 | 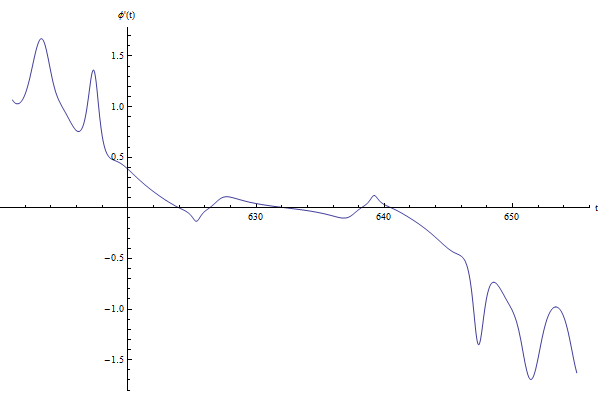 | 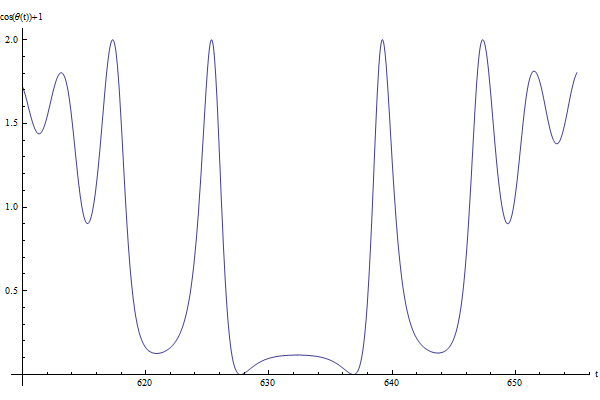 |
$\varphi (t)$ | $\dot{\varphi} (t)$ | $\cos (\theta (t))+1$ |
