Animations
| tracé des trajectoires |
section de Poincaré |
application de premier retour |
distance au point fixe |
courbes φ(t) , φ'(t) , θ (t) , θ'(t) |
complètes instable ! |
Animation 4
Distance au point fixe
Ce programme trace $\cos (\theta (t)) +1$, représentant la distance au cours du temps entre la masse et le point fixe instable $\theta = \pi \; , \; \varphi = 0$ : cette fonction s'annule lorsque $\theta = \pm \pi$ .
On observe que si on lâche le pendule du point fixe instable $\theta = \pi - \mid \alpha \mid \; , \; \varphi = \frac{\pi}{2}$ avec les conditions initiales données dans l'animation ci-dessous, on peut observer une inversion du sens de rotation selon $\varphi$ du pendule lorsque celui-ci passe sur le point fixe instable $\theta = \pi \; , \; \varphi = 0$
Dans le cas présent, la valeur de $\varphi (t)$ ne change pas la distance au point fixe. Il n'est donc pas nécéssaire de tracer la courbe de $[ \varphi (t), 2 \pi ]$ .
Si vous n'arrivez pas à voir le programme, voici quelques images :
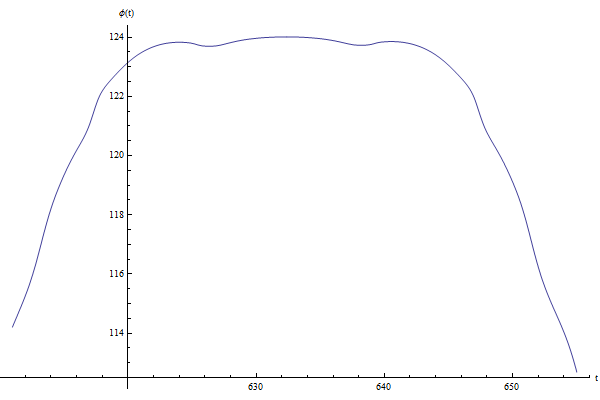 | 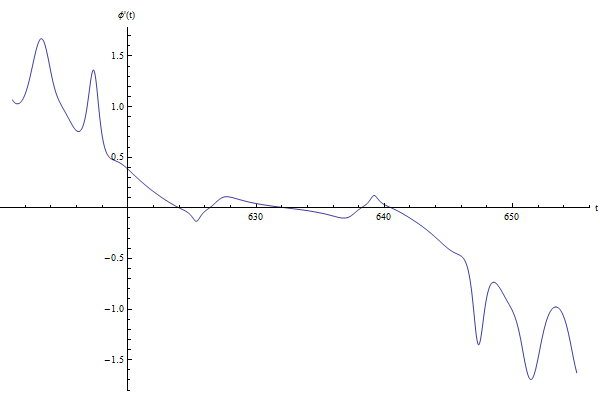 | 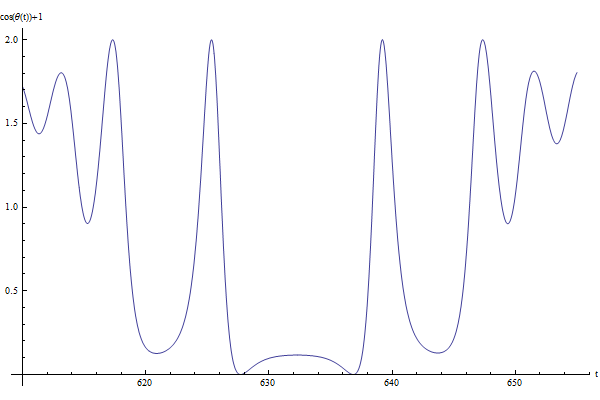 |
$\varphi (t)$ | $\dot{\varphi} (t)$ | $\cos (\theta (t))+1$ |
