LA MOLECULE D'AMMONIAC

Le double puits de potentiel est un exemple que nous avons beaucoup travaillé durant notre projet. Ici, nous traiterons un cas de double puits appliqué à une molécule que l'on connaît bien: l'ammoniac.

Un exemple de couplage est donné par la molécule d'ammoniac NH₃ Cette molécule, de forme tétraédrique possède deux états d'équilibres définis par la position de l'atome d'azote N par rapport au plan, formé par les 3 atomes d'hydrogène. En effet, les liaisons atomiques présentes au sein de la molécule forment un double puits de potentiel qui laisse entrevoir deux minimas et donc deux positions d'équilibres, symétriques.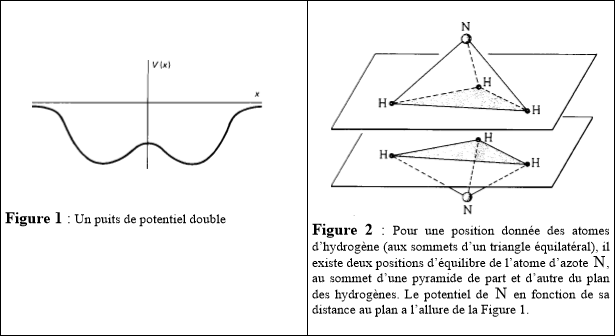

Image tirée du cours de D.Marchand à https://cours.espci.fr/site.php?id=73&fileid=382

Classiquement, la molécule ne peut passer d'un état à l'autre. C'est-à-dire que si l'atome d'azote est d'un côté du plan, il y restera puisque celui-ci se trouve à l'équilibre. Or l'expérience a montré que la molécule passait d'un état à l'autre et donc que l'atome d'azote franchissait effectivement la barrière de potentiel, cela par effet tunnel. On peut étudier ce comportement en construisant la fonction d'onde associé au système physique. D'après le principe de superposition, l'état d'un tel système peut être exprimé comme la combinaison linéaire de tous les états possibles du système (états propres). En vertu de ce que nous avons vu dans l'annexe technique (cf 3.3 de notre rapport, disponible ici), on écrit la fonction d'onde du système :

Où Ψ_(n,S) (x) est la fonction d'onde symétrique du système.
Ψ_(n,A) (x) est la fonction d'onde antisymétrique du système.

NB: Ψ_(n,S) (x) et Ψ_(n,A) (x) forment un système de fonction dit complet. C'est-à-dire que le système ne peut être que dans un des deux états ou dans une combinaison linéaire de ces deux états.

On a aussi d'après l'équation temporelle de SCHRÖDINGER :

Mais puisque Ψ_(n,S) (x) et Ψ_(n,A) (x) sont des états propres du système, on a :

Avec E_(n,S) et E_(n,A) les énergies propres du système. On en déduit immédiatement les expressions:

On peut également décomposer Ψ_(n,S) (x,t=0) et Ψ_(n,A) (x,t=0) en combinaisons linéaires des deux fonctions correspondant à chacun des puits (cf annexe 3.3 de notre article), notées Ψ_(n,G) (x) pour le puits gauche et Ψ_(n,D) (x) pour le puits droit. Il vient donc que :

Finalement, en posant que :

Alors la fonction d'onde peut être écrite comme :

Ou encore:

Nous avons donc établi la fonction d'onde associé au double puits, pour une énergie E_n donnée. On en déduit directement les probabilités de présence de l'atome d'azote dans un des deux puits :

Probabilité que la particule soit dans le puits de droite :

Probabilité que la particule soit dans le puits de gauche :

Remarque : On remarque qu'au temps t=0 la particule se trouve forcément à droite, ce qui est purement arbitraire. Cela dépend de la définition des états antisymétriques, on aurait pu avoir l'inverse en définissant :

Bien-sûr on a :

La particule est se trouve forcément quelque part. (Les barrières extérieures du puits sont infinies, et donc la particule reste confinée dans le puits, ce qui est fort heureux pour la molécule...).

Penchons-nous sur ces probabilités. On remarque que leurs valeurs oscillent avec le temps, si l'on effectue une mesure à un instant t instant quelconque, on aura une probabilité plus ou moindre de trouver la particule dans un des deux puits, en revanche pour certains temps bien précis, on peut déterminer avec certitude la position de notre atome. Prenons l'exemple du puits à droite :

D'où la nécessité de pouvoir calculer ΔE. Pour un tel puits, ce n'est pas chose aisée avec une résolution analytique. C'est ici qu'intervient l'approximation WKB. Nous avions établi dans la partie 3.3 de l'annexe une expression pour ΔE :

Avec [-a;a] la largeur de la barrière au milieu des deux puits, au niveau d'énergie considéré. Il vient donc que :

D'après l'équation (71) de la partie 3.3, on peut réécrire le résultat précédent sous la forme suivante :

On a donc un lien direct entre le temps t et le facteur d'effet tunnel (terme en exponentielle), pondéré par un terme lié à la vitesse de la particule.

Remarque : On sait en physique statistique que la probabilité de trouver la particule dans un élément de longueur dx est proportionnelle à dx/v et donc que le terme en intégrale dans l'exponentielle est lié la probabilité de trouver la particule dans un des deux puits (en l'occurrence le puits droit). On retrouve donc bien des éléments de physique statistique à l'aide de lapproximation WKB.