L'EFFET TUNNEL

L'effet tunnel représente un des concepts les plus importants en physique quantique. C'est pourquoi notre projet s'est globalement concentré autour de cela.


Qu'est-ce que l'effet tunnel? Lorsqu'un objet quantique (ex. un électron) fait face à une barrière de potentiel, celui-ci possèdant une énergie inférieure à la hauteur de la barrière, on s'attendrait à ce que celui-ci "rebondisse" sur la barrière. Or, on a remarqué que la probabilité de trouver l'électron après la barrière n'est pas nulle! Celle-ci va dépendre de plusieurs facteurs, comme l'épaisseur de la barrière ou l'énergie que l'on donne à l'électron. Si l'on se place dans une vision classique, l'effet tunnel représente quelque chose que l'on a du mal à concevoir. C'est pour cela qu'il faut adopter une vision quantique des choses, et revenir à la dualité "onde-corpuscule" d'un électron dont nous avons parlé précédemment.

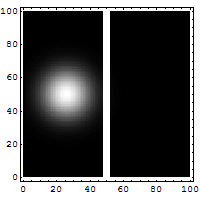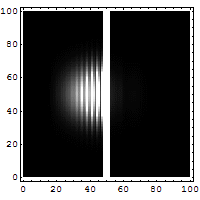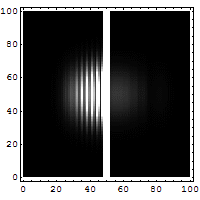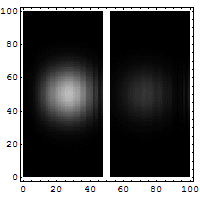Densité de probabilité de l'électron faisant face à une barrière de potentiel

Sur l'image animée ci-dessus, est représentée la densité de probabilité d'un électron qui fait face à une barrière de potentiel. à gauche de l'image, on voit bien que la probabilité que l'électron soit réfléchi est très grande, mais il existe une faible probabilité que l'électron puisse traverser la barrière (représentée à droite de l'image).

Application numérique: Effectuons un raisonnement analytique afin d'exprimer la probabilité qu'a un électron de traverser une barrière de potentiel de hauteur finie, représentée sur l'image suivante:

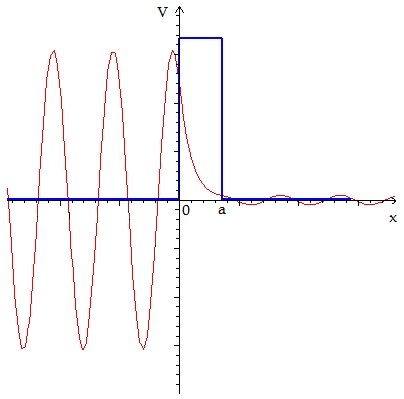Représentation de la fonction d'onde ℜ{Ψ(x)} aux abords d'une barrière de potentiel

À l'aide de l'équation de Schrödinger qui est la suivante:

On obtient des expressions pour la fonction d'onde suivant l'emplacement où l'on se trouve. À gauche de la barrière, le potentiel vaut V=V₀, donc la fonction d'onde est la suivante:

Au sein de la barrière, celle-ci s'écrit:

Enfin, à droite de la barrière, on a:

Ainsi, on en déduit le coefficient de transmission:

Si l'on aborde ce problème avec une approche classique, on devrait s'attendre à ce que le coefficient de transmission de la barrière soit nul. Or, nous venons de voir que celui-ci ne l'est pas. En effet, ce coefficient possède une dépendance en une exponentielle négative qui dépend de la largeur de la barrière a. On retrouve donc bien ce que l'on a dit auparavant: plus l'épaisseur de la barrière est importante, plus le coefficient de transmission de celle-ci tendra vers 0. IL en découle donc que la probabilité de trouver l'électron après le passage de la barrière n'est pas nul, c'est comme cela que l'on observe analytiquement l'effet tunnel.