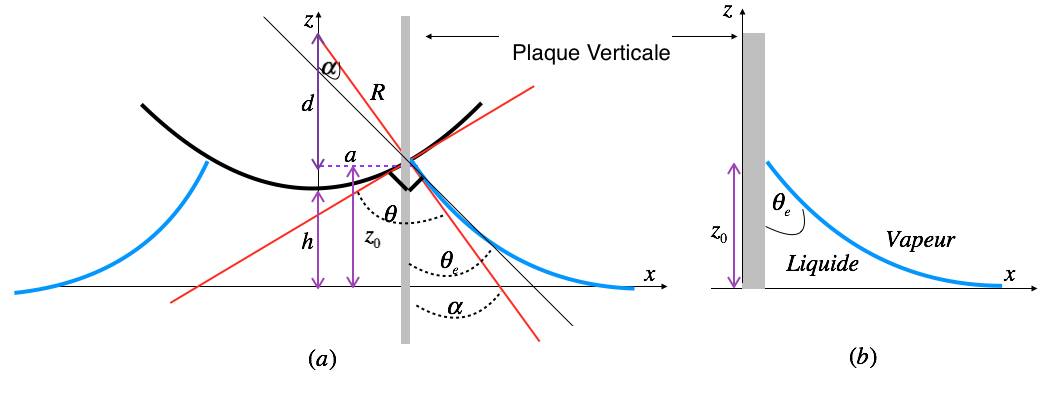
(a) : Raccordement de l’eau sur une surface sphérique formant un pont capillaire. Les droites rouges représentent la tangente à la surface sphérique et la tangente au ménisque statique formant le pont. R est le rayon de courbure de la lentille. a représente le rayon de l’aire réelle mouillée. (b) : Raccord d’un ménisque statique de l’eau sur une plaque verticale formant un angle à l’équilibre θe .
La hauteur du ménisque statique z0 sur un plan vertical a été calculée dans la partie « mouillage et gravité ». Elle est donnée par la formule :
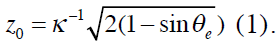 On peut faire l’analogie entre les deux représentations, en supposant que l’on place une
plaque verticale au niveau du point de raccordement entre l’eau et la surface sphérique. Ainsi,
la hauteur de montée du liquide au niveau de la surface sphérique est équivalente à la
hauteur du ménisque statique sur un plan vertical z0 on peut retrouver la valeur de l’angle
de contact du liquide sur le verre qui est égale à :
On peut faire l’analogie entre les deux représentations, en supposant que l’on place une
plaque verticale au niveau du point de raccordement entre l’eau et la surface sphérique. Ainsi,
la hauteur de montée du liquide au niveau de la surface sphérique est équivalente à la
hauteur du ménisque statique sur un plan vertical z0 on peut retrouver la valeur de l’angle
de contact du liquide sur le verre qui est égale à :
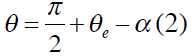 où θe est l’angle avec
lequel ce liquide se raccorderait sur une surface plane de même nature.
où θe est l’angle avec
lequel ce liquide se raccorderait sur une surface plane de même nature.Sur la figure ci-dessus on peut déduire la relation de Pythagore suivante :
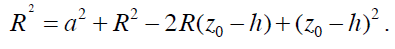
Comme (z0 − h) << R , on trouve :
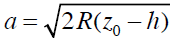
Or l’aire mouillée est : A =π a2 ce qui donne A=2π R(z0 - h).
D’après la formule (1) et en isolant θe de la relation (2), on trouve :
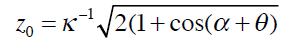
Comme
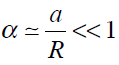 , on retrouve finalement :
, on retrouve finalement :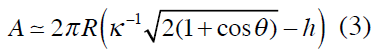
La relation (3) n’est valide que pour des rayons de courbures grands devant la longueur capillaire et pour des angles de contact pas trop petits.
La partie linéaire de l’aire mouillée A en fonction de la hauteur entre le bain d’eau et le verre a pour pente égale à 2π R . Donc la pente des droites correspondantes au cycle tirage-enfoncement dépend uniquement du rayon de courbure du verre.
L’ordonnée à l’origine des droites en h=0 est donnée par :
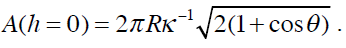
L’analyse des courbes expérimentales A=f(h) doit donc permettre de déterminer l’angle de contact du liquide sur la surface à partir de l’aire de contact initiale A0 étant donné que la longueur capillaire est connue pour un liquide.
On a vu précédemment que lorsqu’on vient tirer le verre du bain d’eau, on observe un plateau où l’aire de contact reste constante. L’aire diminue ensuite linéairement en fonction de la hauteur lorsque l’angle de contact atteint l’angle de reculée. Donc, en h=0 on a
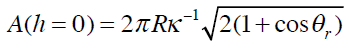
Ayant la valeur de la pente à partir des droites de nos cycles et l’ordonnée à l’origine des droites A(h=0) on peut déduire l’angle de reculée. Si on inverse le mouvement et que le verre est cette fois enfoncé vers le bain de l’eau, on observe de nouveau un plateau identique au premier, où l’aire de contact reste constante. Lorsque la ligne de contact avance, l’aire augmente linéairement en fonction de la hauteur. L’angle de contact qui était égale à l’angle de reculée devient maintenant égale à l’angle d’avancée. Donc, en h=0, en a
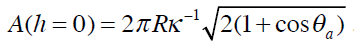 . De la même manière on déduit l’angle
d’avancée.
. De la même manière on déduit l’angle
d’avancée.