Cycle Tirage-Enfoncement

Dans la partie précédente, nous avons présenté le résultat typique pour une séquence de tirage simple. On réalise cette fois un cycle de tirage-enfoncement en traçant l’aire de contact en fonction de la hauteur h . En effet, tant que la vitesse de tirage est suffisamment faible, il est possible d’arrêter le mouvement de tirage du verre avant que le pont capillaire ne casse et de ré-enfoncer la surface solide dans le bain d’eau distillée.
Les parties (A), (B) et (C) sont celles qui ont été décrites dans le cas d’un tirage simple. Si cette fois on inverse le mouvement du solide avant que la hauteur n’atteigne sa valeur finale, on observe de nouveau un plateau et une progression constante de l’aire de contact (A1). Ce plateau est due au fait que la ligne triple reste piégée à l’endroit où on a inversé le mouvement de la surface. Ainsi, la ligne n’avance pas tant que l’angle de contact qui est cette fois égal à l’angle de reculée n’a pas atteint l’angle d’avancée. Lorsque cette condition est réalisée, l’aire de contact croit ensuite linéairement avec la hauteur h de manière similaire à la décroissance de l’aire de contact observée pour une expérience de tirage simple de la lentille (B1). Les 2 droites (B) et (B1) sont parallèles et ont la même pente. Le seul point différent entre les droites correspondantes au tirage et à l’enfoncement du verre est leur ordonnées à l’origine. En fait, dès que la ligne triple est dépiégée, c’est-à-dire dès que l’angle de contact a atteint l’un de ses valeurs extrêmes (angle d’avancée ou de reculée) selon le sens de déplacement du verre, l’aire croit ou décroit linéairement avec la distance h, en adoptant la même pente pour les deux droites. Si on inverse de nouveau le mouvement et qu’on tire de nouveau la lentille vers le bain d’eau distillée, un autre plateau est observé (A2). Il est parallèle à (A1) et est également de même longueur. Les plateaux (A1) et (A2) sont donc directement liés à l’hystérèse de l’angle de contact. A partir de ces courbes, on peut alors extraire les caractéristiques de la partie linéaire qui sont la pente et l’ordonnée à l’origine. On montrera dans la partie analyse et discussion comment il est possible à partir des courbes expérimentales A=f(h) de déduire les angles de contact d’avancée et de reculée.


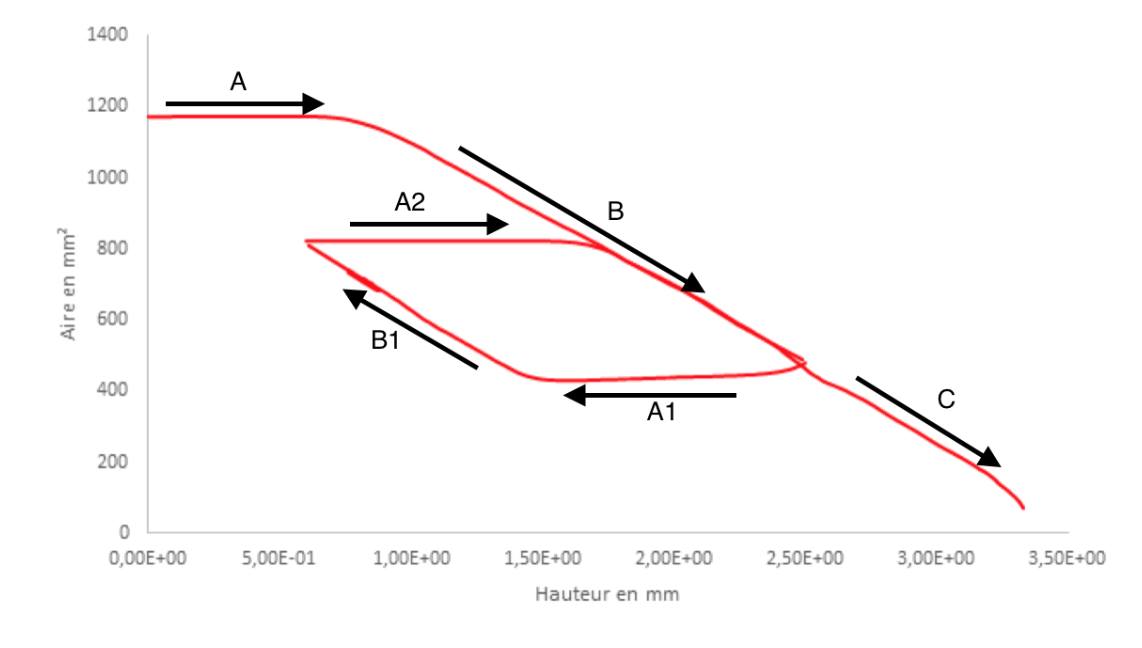cycle Courbes représentatives de l’évolution de l’aire en fonction de la distance h entre un bain d’eau distillée et une surface solide (PDMS 750 pour ce graphe). Les flèches indiquent le sens de déplacement de la surface par rapport au liquide lors de l’expérience. Les parties A, B, A2 et C correspondent à des séquences de tirage et les parties A1 et B1, correspondent à des séquences d’enfoncement.