Le code commence avant tout par ouvrir les fichiers dans lesquels nous allons écrire et déclarer toutes les variables : qu'elles soient des entiers (int) ou des nombres décimaux (double).
Puis, il acquiert les différentes variables de contrôle, alloue de façon dynamique la mémoire, lit les configurations initiales produites par le code CONF.IN.c et enfin démarre la boucle principale.
La boucle principale se décompose en plusieurs points: En fonction d'une particule i,
Nous trions toutes les particules selon leur rayon, celles qui sont plus grandes que i et celles qui sont plus petites.
Le tri se fait selon le principe du tri rapide: la fonction choisit une particule pivot qui est notre i au début et classe. Ensuite, quand cela est rangé,
elle recommence avec un autre pivot qu'elle prend soit dans la partie inferieure à i soit dans la supérieure.
Ainsi de suite, jusqu'à ce que tout soit trié.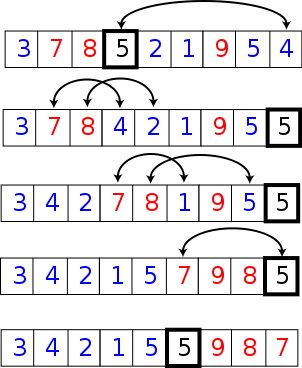 
Le point précèdent va nous aider à calculer la force de façon plus rapide. Dans ce code la force exercée
sur une particule est la résultante des forces exercées par toutes les autres.
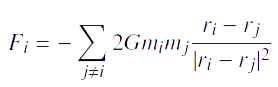
ce qui se traduit en code par trois étapes :
1) calculer la distance entre la particule i et celle (j) qui va exercér une force : dx=rx[i]-rx[j]; dy=ry[i]-ry[j]; => r2=dx*dx+dy*dy+e*e;( le e de epsilon n'apparait pas dans l'expression de la force. Nous l'avons rajouté pour éviter la divergence à certains endroits.)
2) calculer la force de j sur i : fij=-2.*G*m*m/r2;
3) sauvegarder ce calcul dans un tableau des forces (la ième case contenant la force qui s'applique sur la ième particule)
fx[i]=fx[i]+dx*fij;
fy[i]=fy[i]+dy*fij;
fx[j]=fx[j]-fij*dx;
fy[j]=fy[j]-fij*dy;
La derniè étape consiste à calculer à partir de la force qui s'applique à chaque particule, leur nouvelle position et leur nouvelle vitesse.
Ceci est réalisé grâce à l'Algorithme de Verlet : 
et pour les vitesses 
en code cela se décompose en plusieurs étapes:
1) stocker dans une variable temporelle la position actuelle de i;
2) calculer la nouvelle position : rx[i]=2.0*rx[i]+2.0*c1*fx[i]/m-rax[i]; par la formule de Verlet.
3) calculer la nouvelle vitesse : vx[i]=(rx[i]-rax[i])/(2*c0);
4) stocker la position précèdente dans un tableau afin de pouvoir s'en servir au 2ème pas;
5) réinitialiser les forces à 0.
6) calculer l'énergie cinétique;
Attention dans notre cas, l'accélération est assimilée à la force,
ceci du aux conditions initiales m=1.0.