Identification du paramètre d’équilibre thermodynamique ξ(t)
Nous allons pouvoir observer si l’équilibre thermodynamique a été atteint.
Pour cela, nous avons tracé la distribution des vitesses en fonction des particules pour chacune de nos deux simulations à l’aide des deux forces.
Simulation 1
Vo= 1.0/1.7
Ro=1.0
•Force exacte entre deux particules
Nous ne pouvons pas avoir de résultat pour la force 1, car étant donné que nous n’avons pas fait tourner le programme assez longtemps, le résultat que nous aurions obtenu n’aurait eu aucun intérêt.
En effet, l’importance de pouvoir tracer les probabilités de vitesses et donc le paramètre ξ(t) est de pouvoir observer l’évolution vers l’état d’équilibre, ce que nous ne pouvons constater pour une courte simulation.
•Force à symétrie polaire
Cette simulation a été réalisé pour 8000 prarticules.
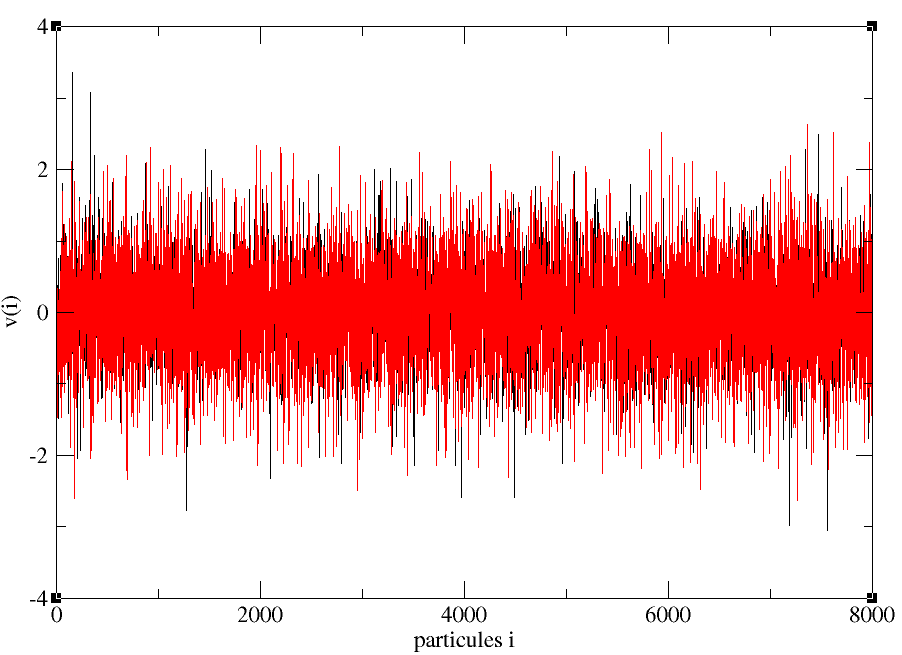
Figure 16 – Distribution des vitesses en fonction des particules
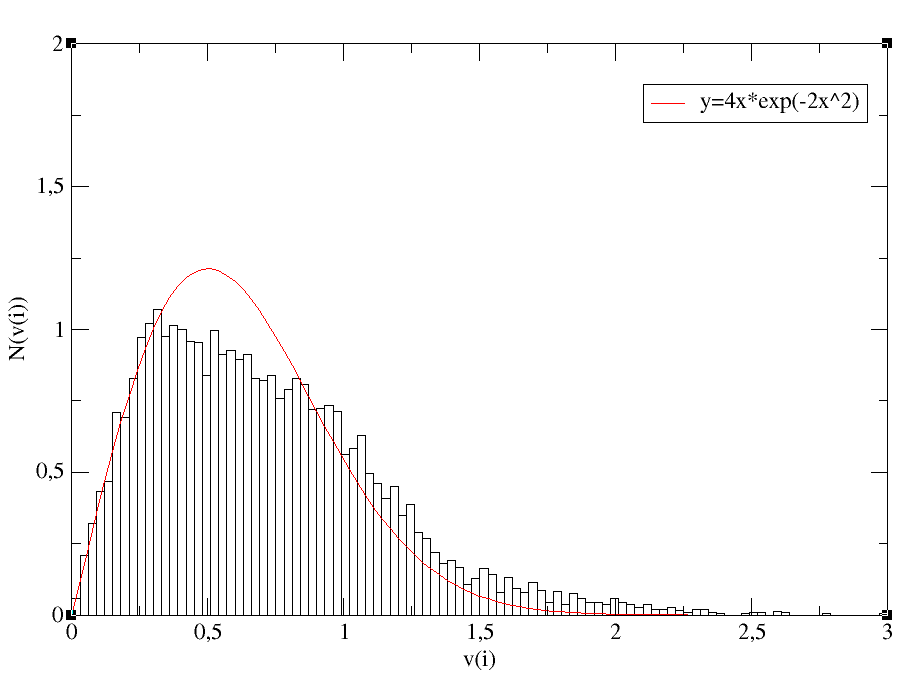
Figure 17 – Histogramme de la distribution des vitesses
Nous avons tracé 10 histogrammes comme celui-ci pour des temps différents, ce qui nous a permis de sortir le paramètre ξ(t)
qui régit notre équilibre thermodynamique.
Nous pouvons donc observé d’après ce graphique que l’état d’équilibre thermodynamique n’est pas
encore atteint. En effet, nous devrions nous attendre à un ξ(t) qui décroit bien distinctement et ce n’est
pas le cas ici.
Nous pouvons en conclure que le système n’a pas eu le temps d’évoluer assez suffisamment et que nous nous trouvons
encore dans l’état quasi–stationnaire
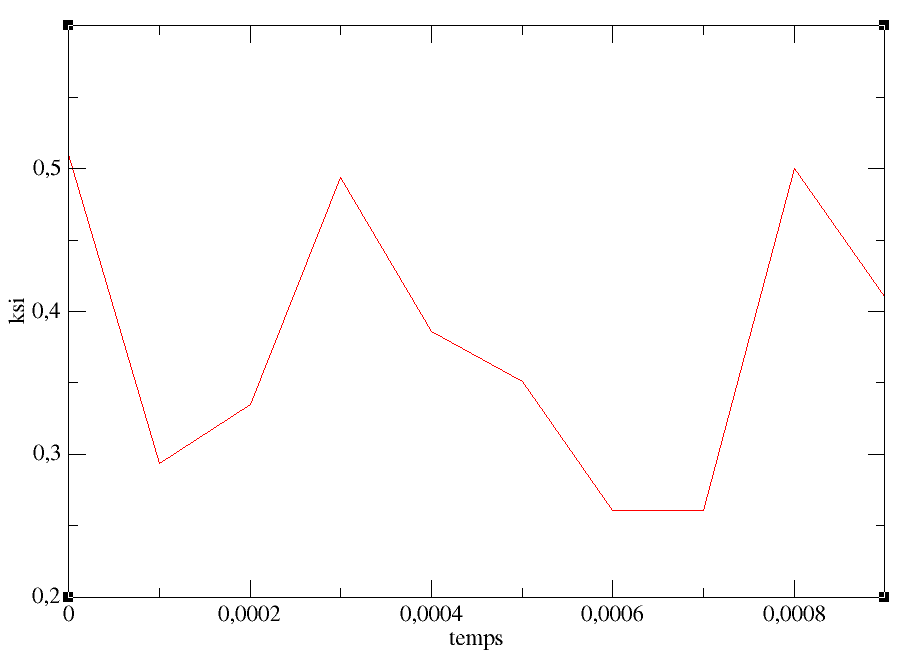
Figure 18 – Représentation du paramétre d’équilibre en fonction du temps : ξ(t)





