Tout d’abord, nous nous plaçons en dimension 3. Pour trouver l’expression des forces et des potentiels qui vont régir les mouvements des particules, nous partons de l’équation de Poisson. Expérimentalement, nous connaissons l’expression de la force gravitationnelle:
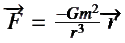
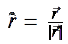
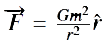
Nous définissons l’expression du champs gravitationnel par :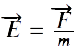 
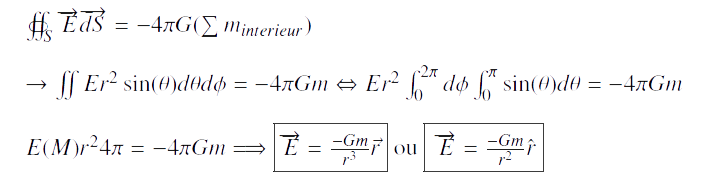
Si nous multiplions cette expression du champ par la masse, nous retrouvons bien l’expression expérimentale de la force gravitationnelle. À partir du champs gravitationnel que nous avons calculé nous pouvons démontrer l’ expression de l’équation de Poisson en dimension 3.
En calculant la divergence de E, nous avons:
L’ expression (1) n’est pas bien définie pour r=0, nous allons donc étudier la divergence de E au voisinage de r=0.
Pour ce faire, nous allons calculer l’intégrale suivante pour une sphère de rayon ε :
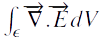Or par le théorème du flux–divergence, nous avons: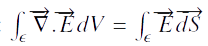 
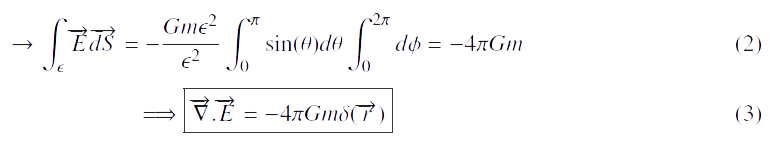
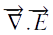comme l’expression (3), qui présente
les propriétés de (1) et (2) car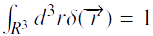 
par définition du dirac δ.
Nous avons démontré l’expression de l’équation de Poisson en dimension 3 et
maintenant nous nous intéressons à un modèle de gravitation en deux dimensions.
Pour cela, nous calculons la force gravitationnelle exercée entre deux fils infinis parallèles.
Nous démontrons l’expression du champ gravitationnel en dimension 2 avec le théorème de Gauss:
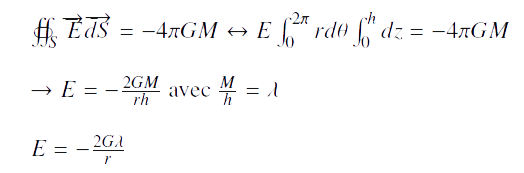Dans notre cas, nous posons : 
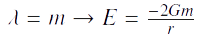Et nous trouvons: 
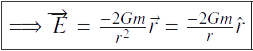Pour se rapprocher le plus de notre problème, nous considérons que les fils se maintiennent parallèles entre eux au cours du temps.
Nous pouvons les assimiler à deux points de masse m intéragissant avec la force.
En effet, il nous apparait maintenant des petits cercles et nous savons que le champ gravitationnel crée par les deux fils infinis sera le même
pour deux cercles vu de haut.
Nous pouvons vérifier que ce champ entre deux fils satisfait l’équation de poisson:
Par le calcul de la divergence, nous obtenons :
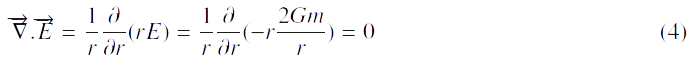De même que pour un système en dimension 3, nous étudions la divergence de E au voisinage de r=0.
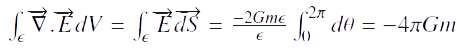Pour une particule : 
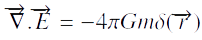Pour n particules : 
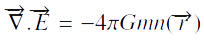Avec m comme étant la masse et n la densité de particules, d’oú m*n est la densité de masse.
Nous remarquons que l’équation de Poisson est la même pour un système 3-D et pour un système 2-D.