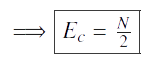Pour un système en 3-D, le théorème du Viriel nous permet d’établir une relation entre l’énergie cinétique et l’énergie potentielle d’un système stationnaire à plusieurs particules en intéraction, c’est-à-dire qu’il n’évolue pas au cours du temps.
Nous savons que le résultat en 3-D est :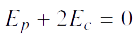 
et nous allons démontrer le résultat en 2-D qui est en accord avec notre étude.
Selon le principe fondamental de la dynamique, la force gravitationnelle s’écrit pour chaque corps i :
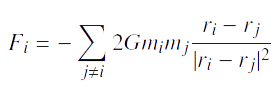
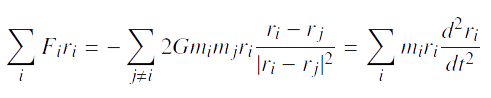Avec: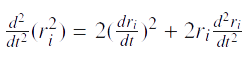 
Et sachant que si nous échangeons les indices muets, nous avons:
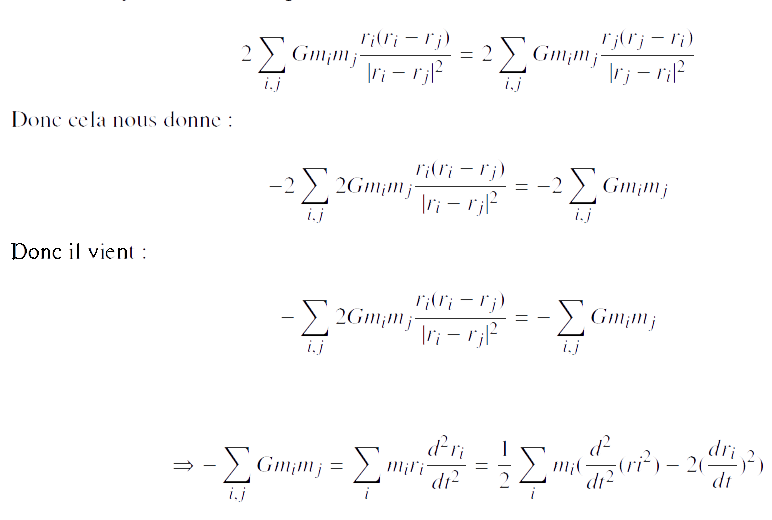On reconnait dans cette équation la dérivée seconde du moment d’inertie:
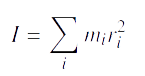Or à l’équilibre nous avons I=0 ,
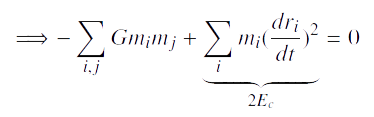
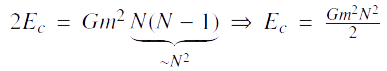Or nous avons posé : 
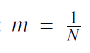car nous ne voulons pas que l’accélération dépende de N.
De plus, G=1 et dans le code que nous avons écrit, nous traçons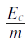 
et non Ec, c’est pour cela que dans les résultats que nous obtiendrons, nous nous attendrons à avoir:
