Énergies Cinétiques
Nous allons observer les énergies des deux simulations et comparer pour chacune d’elle
les résultats obtenu pour les deux programmes utilisés
Un premier résultat que nous obtenons est celui de l’énergie cinétique en fonction du temps.
Comme nous l’avons montré théoriquement, une fois que l’état quasi–stationnaire est atteint, nous devrions
nous attendre à ce que l’énergie cinétique tende vers une valeur constante.
Tout d’abord, nous pouvons montrer que pour un temps court, l’énergie oscille bien comme nous devrions
nous y attendre :
Simulation 1
Vo= 1.0/1.7
Ro=1.0
•Force à symétrie polaire
Voici le résultat pour 8000 particules:
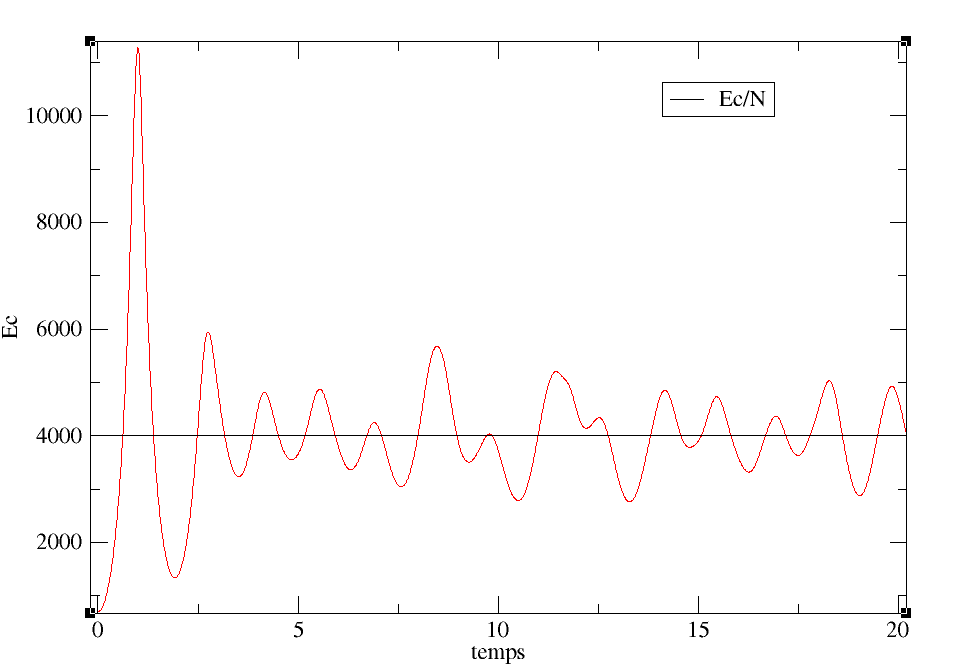
Figure 5 – Zoom de l’énergie cinétique pour N = 8000 particules
Nous remarquons que l’énergie cinétique tend bien vers la valeur
constante attendu selon le théorème de Viriel :
En effet, cette énergie cinétique a été tracé pour
8000 particules et elle tend vers la moitié, soit 4000, lors de l’état quasi–stationnaire.
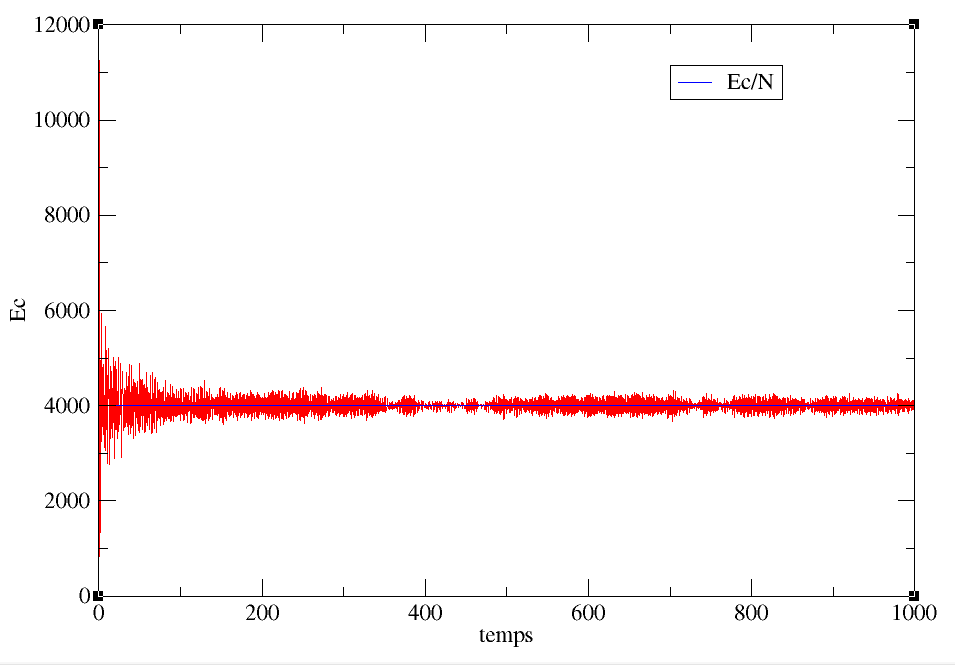
Figure 6 – Énergie cinétique pour N = 8000 particules
Voici le résultat pour 1000 particules:
_1000.png)
Figure 7 – Zoom de l’énergie cinétique pour N = 1000 particules
_1000.png)
Figure 8 – Énergie cinétique pour N = 1000 particules
Simulation 2
Vo= 1.0
Ro=1.0
•Force à symétrie polaire
Voici le résultat que nous obtenons pour la simulation 2, l’énergie tend bien vers la constante du Viriel.
_1000.png)
Figure 9 – Énergie cinétique pour N=1000 particules
Nous remarquons que le théorème de Viriel est bien vérifié, nous pouvons dire que le code exact
valide très bien le code approché.
