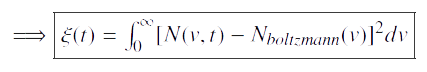Probabilités de vitesse
Pour un système thermodynamique, nous connaissons la probabilité de vitesse:
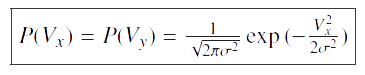
Par le théoème du Viriel, nous trouvons:
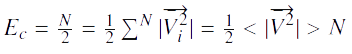
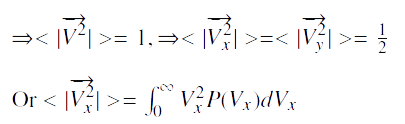
Nous voulons déterminer σ; par le calcul de cette vitesse moyenne, nous avons:
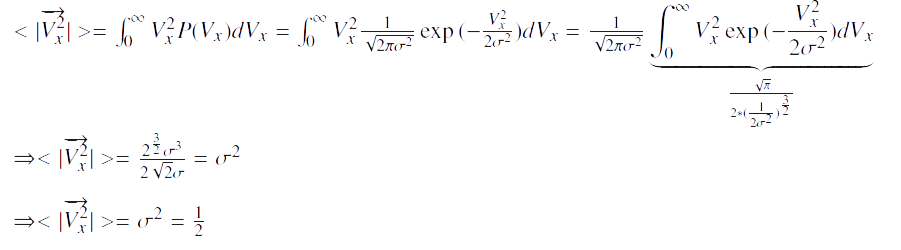
Nous trouvons la valeur de σ à laquelle nous devons nous attendre pour un équilibre thermodynamique:

Il s’agit donc de la valeur de la largeur de notre gaussienne de probabilité pour un équilibre thermodynamique.
Pour le moment, nous ne connaissons que les probabilités de vitesse pour Vx et Vy, mais nous pouvons démontrer la probabilité de vitesse de V.
Nous savons que :
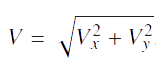
d’oú :
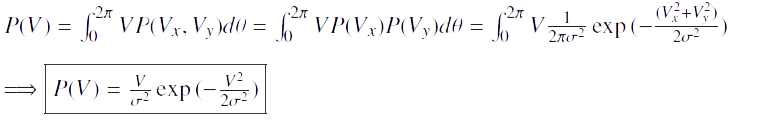
Nous allons maintenant utiliser une nouvelle fonction ξ(t) qui va nous permettre d’étudier l’évolution d’un système de particules tendant vers un équilibre de Boltzmann.
Pour caractériser cet équilibre, deux paramètres peuvent être pris en compte:
- La distribution des vitesses
- La distribution des positions
La distribution des positions étant difficile à calculer à l’équilibre thermodynamique, nous avons choisi de créer une fonction ξ(t) qui mesurera la différence entre la distribution des vitesses du système à un instant t et celle théorique de Boltzmann que nous connaissons être sous forme gausienne.
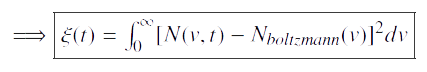



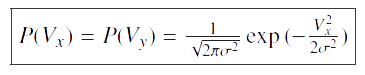 Par le théoème du Viriel, nous trouvons:
Par le théoème du Viriel, nous trouvons: 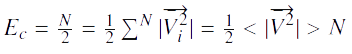
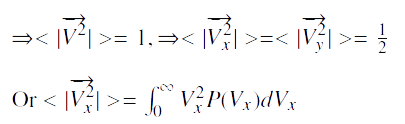 Nous voulons déterminer σ; par le calcul de cette vitesse moyenne, nous avons:
Nous voulons déterminer σ; par le calcul de cette vitesse moyenne, nous avons:
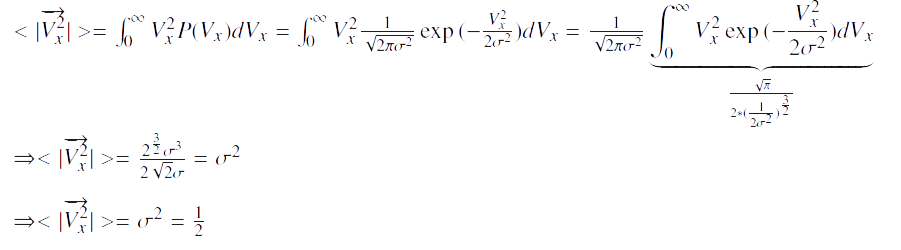 Nous trouvons la valeur de σ à laquelle nous devons nous attendre pour un équilibre thermodynamique:
Nous trouvons la valeur de σ à laquelle nous devons nous attendre pour un équilibre thermodynamique:
 Il s’agit donc de la valeur de la largeur de notre gaussienne de probabilité pour un équilibre thermodynamique.
Pour le moment, nous ne connaissons que les probabilités de vitesse pour Vx et Vy, mais nous pouvons démontrer la probabilité de vitesse de V.
Nous savons que :
Il s’agit donc de la valeur de la largeur de notre gaussienne de probabilité pour un équilibre thermodynamique.
Pour le moment, nous ne connaissons que les probabilités de vitesse pour Vx et Vy, mais nous pouvons démontrer la probabilité de vitesse de V.
Nous savons que : 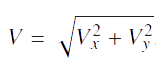 d’oú :
d’oú :
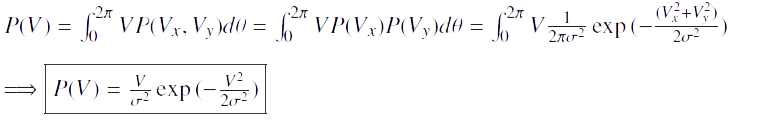 Nous allons maintenant utiliser une nouvelle fonction ξ(t) qui va nous permettre d’étudier l’évolution d’un système de particules tendant vers un équilibre de Boltzmann.
Pour caractériser cet équilibre, deux paramètres peuvent être pris en compte:
- La distribution des vitesses
- La distribution des positions
La distribution des positions étant difficile à calculer à l’équilibre thermodynamique, nous avons choisi de créer une fonction ξ(t) qui mesurera la différence entre la distribution des vitesses du système à un instant t et celle théorique de Boltzmann que nous connaissons être sous forme gausienne.
Nous allons maintenant utiliser une nouvelle fonction ξ(t) qui va nous permettre d’étudier l’évolution d’un système de particules tendant vers un équilibre de Boltzmann.
Pour caractériser cet équilibre, deux paramètres peuvent être pris en compte:
- La distribution des vitesses
- La distribution des positions
La distribution des positions étant difficile à calculer à l’équilibre thermodynamique, nous avons choisi de créer une fonction ξ(t) qui mesurera la différence entre la distribution des vitesses du système à un instant t et celle théorique de Boltzmann que nous connaissons être sous forme gausienne.