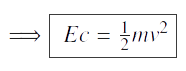Force et potentiel à symétrie polaire
L’expression de la force entre deux particules correspondait au calcul exact de la force et nous en avons déduit le potentiel.
Dans cette partie, nous allons calculer une nouvelle expression de la force en imposant que le système soit sphérique. Nous définissons la force par rapport à la masse.
Nous considérons le champ crée par une distribution de charges surfaciques à l’intèrieur d’un rayon r.
D’oú comme
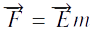
L’expression de la force devient :
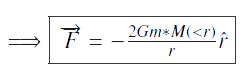
Oú M(‹ r) représente la masse des particules qui se trouvent à l’intèrieur du cercle de rayon r.
Dans ce cas-là, la direction des forces est importante et est donc à prendre en compte dans l’étude numérique.
Nous en déduisons une nouvelle expression du potentiel :
Posons
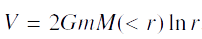
Et si nous calculons
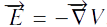
Cela vérifie bien l’expression du potentiel.
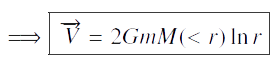
L’expression de l’énergie cinétique reste la même :
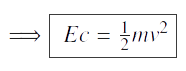



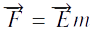 L’expression de la force devient :
L’expression de la force devient :
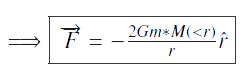 Oú M(‹ r) représente la masse des particules qui se trouvent à l’intèrieur du cercle de rayon r.
Dans ce cas-là, la direction des forces est importante et est donc à prendre en compte dans l’étude numérique.
Nous en déduisons une nouvelle expression du potentiel :
Posons
Oú M(‹ r) représente la masse des particules qui se trouvent à l’intèrieur du cercle de rayon r.
Dans ce cas-là, la direction des forces est importante et est donc à prendre en compte dans l’étude numérique.
Nous en déduisons une nouvelle expression du potentiel :
Posons 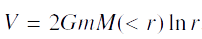 Et si nous calculons
Et si nous calculons 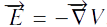 Cela vérifie bien l’expression du potentiel.
Cela vérifie bien l’expression du potentiel.
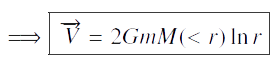 L’expression de l’énergie cinétique reste la même :
L’expression de l’énergie cinétique reste la même :